 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Применение формул Крамера и решению систем линейных уравнений
Рассмотрим применение формул Крамера к решению систем двух линейных уравнений с двумя неизвестными.

Решение. Вычислим определитель системы и определители х и у:

Найдем значение х и у по формуле Крамера:

Итак, решение системы есть (3:-1).
72. Решите систему уравнений

Решение. Вычислим определитель системы и определители х и у:

Так как =0, а х≠0, у≠0, то система не имеет решений (уравнения противоречивы).
73. решить систему уравнений

Решение. Находим

Данная система имеет бесчисленное множество решений (коэффициенты при неизвестных пропорциональны).
74. Решить систему уравнений

Решение. Вычислим определить системы и определители при неизвестных:


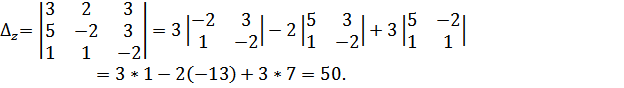
Найдем значения x, y, z по формулам Крамера.

Итак, получаем ответ: (1;-1;2).
Тема 3. Решение систем линейных уравнений методом Гаусса.
При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвестных). Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
1. Умножение или деление коэффициентов свободных членов на одно и то же число;
2. Сложение и вычисление уравнений;
3. Перестановку уравнений системы;
4. Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободных членов равны нулю.
Используя метод Гаусса, решить систему уравнений.

Решение. Переставим третье уравнение на место первого:

Запишем расширенную матрицу:

Что бы в 1-м столбце получить а21=а31=0, умножим 1-ю строку на 3, а затем на 2 вычтем результаты из 2-й и 3-й строк:

Разделим 20-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки:
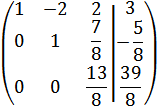
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:
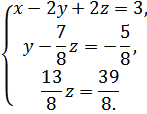
Выполняя обратный ход, с помощью последовательных подставок находим неизвестные:

Итак, получаем ответ: (1; 2: 3).
Поиск по сайту: