Виды и способы задания графов

Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты называются вершинами и обозначаются точками, а связи – дугами. Такие системы образуют графы. Например: граф изображает сеть улиц а городе; сеть дорог, трубопроводов, блок – схемы программирования и многие другие модели.

Определение. Графом называется совокупность двух множеств – непустого множества V вершин и множество Е двухэлементных подмножеств множества V (множество ребер Е).

Обозначаются G(V,E) = <V;E>,V≠O

Множество двух элементных подмножеств определяет симметричное бинарное отношение на множестве Е = V×V, E = E^-1; поэтому ребро можно считать не только как множество 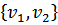, но и как пару число вершин обозначают Р, число ребер – q; если дугами являются пары вершин 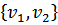то дуга считается исходящей из v₁ и заходящей в v₂; граф G изображают диаграммой.

2

1 V = - множество вершин

3 Е = -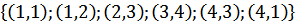

Множество дуг

Если имеется несколько дуг, исходящих из вершины v₁ в вершину v₂, такие дуги называются кратными, граф называется кратным.

Если все элементы множества Е – упорядоченные пары, то граф G называется ориентированным (орграф), элементы V называются узлами, а множество Е дугами, т.е. если (а, b) E, (b, a) ∉ E

Если элементом Е может быть пара одинаковых (не различных) элементов V, то такой элемент называется петлей, а граф называется графом с петлями (псевдографом). Если Е содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами, a G - мультиграфом.

Если (а, b) E /\ (b, a) E, то G называется неориентированным (неографом). В этом случае дуга называется ребром и обозначается в виде отрезка, соединяющего вершины, а вершины а и b называются концами ребра 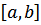и информацию об этих дугах пишут: =

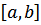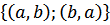
или 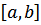- ребро графа

Поиск по сайту: