 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Рассмотрим две прямые
L1: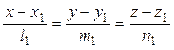 
L2: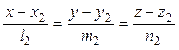 
,если прямая L1 параллельна L2 , то выполняется условие:
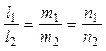(4)
5.) Условие перпендикулярности прямых
l 1 l2 + m1 m 2 +n1 n2 =0 (5)
6). Общее уравнение плоскости
Ax + By + Cz+D = 0, (6)
где A, B, C, D – координаты вектора нормали, причем хотя бы одно из чисел A, B, С отлично от нуля, (x;y;z) - координаты любой точки на плоскости. Геометрический смысл коэффициентов А, В, С в уравнении (1) – это проекции вектора, перпендикулярного плоскости.
7.) Уравнение плоскости, проходящей через три точки
M0 (x0,y0,z0), M1 (x1,y1,z1), M2 (x2,y2,z2)
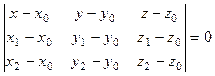(7) или
(x-x0) ((y1-y0)(z2-z0)-(y2-y0)(z1-z0)) – (y-y0) ((x1-x0)(z2-z0)-(x2-x0)(z1-z0))+
+(z-z0) ((x1-x0)(y2-y0)-(x2-x0)(y1-y0))=0
8). Условие параллельности плоскостей
Поиск по сайту: