АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Рассмотрим две плоскости

Читайте также:
  1. Векторы на плоскости
  2. Вопрос 1 Корреляционные функции и спектральные плоскости.
  3. Вопрос27 Полярная и декартова системы координат на плоскости. Связь между полярными и декартовым системами координат. Цилиндрические и сферические системы координат на плоскости.
  4. Восприятие точки, линии, пятна на плоскости
  5. ВОСПРИЯТИЕ ФОРМЫ НА ПЛОСКОСТИ
  6. Вращение плоскости поляризации
  7. Вращение плоскости поляризации
  8. Вращение плоскости поляризации. Оптически активные вещества. Удельное вращение. Поляриметрия (сахариметрия)
  9. Глава III. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ
  10. Дз № 4. Кривые на плоскости
  11. Дз №3. Прямая на плоскости
  12. Закон Брюстера. Вращения плоскости поляризации

Р1: A1 x+B1 y+C1 z+D1=0

Р2:A2x+B2y+C2z+D2=0, если плоскость Р1 параллельна Р2, то выполняется условие:

(8)

9.) Условие перпендикулярности плоскостей

A1 A2 + B1B 2 + C1 С2 =0 (9)

10.а) угол между плоскостями

A1 x+B1 y+C1 z+D1=0 и A2 x+B2 y+C2 z+D2=0

(10.а)

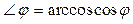
10.б) угол между векторами

и

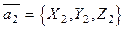
(10.б)

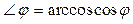
10.в) угол между прямой и плоскостью

прямая L с направляющими коэффициентами (l, m, n) и плоскость Ax+By+Cz+D=0

(10.в)

11.) Расстояние между двумя точками

Даны точки А1 (x1,y1,z1) и А2 (x2,y2,z2), расстояние между ними:

(11)

12.) Расстояние от точки M0 (x0,y0,z0) до плоскости

A x+B y+C z+D=0:

(12)

13.) Выражение векторного произведения через координаты сомножителей, если 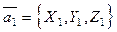, , то

(13)

Первая строка определителя состоит из координатных ортов, вторая из проекций первого сомножителя, третья из проекций второго сомножителя.

14.) Объем параллелепипеда, построенного на векторах

, ,

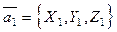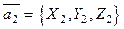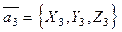
(14)

знак выбирается таким образом, чтобы объем был положительный.

Рассмотрим несколько примеров применения приведенных формул.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)