АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 3. Воспользуемся формулой (11)

Читайте также:
  1. VI. Общая задача чистого разума
  2. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  3. Глава 10 Системный подход к задачам управления. Управленческие решения
  4. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  5. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  6. Двойственная задача линейного программирования.
  7. Доклад о задачах власти Советов
  8. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  9. Задача 1
  10. Задача 1
  11. Задача 1
  12. ЗАДАЧА 1

Даны точки А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2), А 4 (0,1,1).

3.а.) Найти длину ребра А1 А2.

Воспользуемся формулой (11). Расстояние между двумя точками.

Длина ребра А1 А2 равна 3.

3.б.) Составить уравнение ребра А1 А4.и грани А1А2А3 .

Составим уравнение прямой проходящей через точки

А 1 (1,-1,-2) и А 4 (0,1,1), воспользуемся формулой(2)

;

Найдем уравнение плоскости, проходящей через точки

А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2),

 

Воспользуемся формулой (7)

уравнение грани 6 x-8y+5z-4=0, ребра

3.в) Составить уравнение высоты опущенной из точки

А 4 (0,1,1) на плоскость А1А2А3 .

Высота проходит через точку А 4 (0,1,1) иперпендикулярна плоскости 6 x-8y+5z-4=0, имеющей вектор нормали .

Направляющий вектор высоты совпадает с вектором нормали данной плоскости, следовательно т.к. 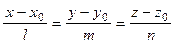(2), то 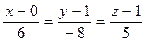уравнение искомой высоты.

или в параметрической форме (3)

x=6t, y=1-8t, z=1+5t

3.г.) Найти площадь треугольника А1A2A3 с вершинами

А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2),

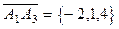Площадь треугольника будет равна 1/2 площади параллелограмма, построенного на векторах и . Площадь параллелограмма равна модулю векторного произведения этих векторов. Воспользуемся формулой (13)

;

,

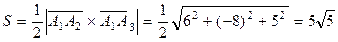
3.д) Найти объем треугольной пирамиды А1A2А3A4 с вершинами

А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2), А 4 (0,1,1).

Искомый объем равен 1/6 объема параллелепипеда, построенного на ребрах А1A2, А1A3, А1A4. Воспользуемся формулой (14)

, ,


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

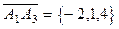Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)