 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
1. Контрольная работа выполняется печатным способом.
2. На титульном листе работы должны быть указаны фамилия, имя, отчество студента, шифр группы, названии дисциплины, факультет, ВУЗ. В начале работы указывается вариант контрольной работы. В конце работы ставится дата ее выполнения и подпись студента.
3. В работу включаются все задачи, указанные в заданиях, и строго по положенному варианту.
4. Условия задач приводятся полностью. Решения излагаются подробно, объясняются все действия по ходу решения.
5. После получения проверенной работы исправляются все отмеченные рецензентом ошибки.
6. Выбор варианта контрольной работы производится по двум последним цифрам номера зачетной книжки в соответствии со следующей таблицей.
| Предпоследняя цифра x совпадает с одной из цифр: 0, 2, 4, 6, 8 | Предпоследняя цифра x совпадает с одной из цифр: 1, 3, 5, 7, 9 |
| х 1 – 1-й вариант х 2 – 2-й вариант х 3 – 3-й вариант х 4 – 4-й вариант х 5 – 5-й вариант х 6 – 6-й вариант х 7 – 7-й вариант х 8 – 8-й вариант х 9 – 9-й вариант х 0 – 10-й вариант | х 1 – 11-й вариант х 2 – 12-й вариант х 3 – 13-й вариант х 4 – 14-й вариант х 5 – 15-й вариант х 6 – 16-й вариант х 7 – 17-й вариант х 8 – 18-й вариант х 9 – 19-й вариант х 0 – 20-й вариант |
 |
- ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задачей линейного программирования (ЗЛП)называется задача, математическая модель которой имеет вид:
(1)
(2)
(3)
(4)
Система линейных уравнений (2) и неравенств (3), (4), определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция 
называется целевой функцией, или критерием оптимальности.
В частном случае, если 
, то система (2) - (3) состоит только из линейных неравенств, а если 
, то — из линейных уравнений.
Рассмотрим процесс построения математических моделей задач линейного программирования на примере.
Пример. Определение оптимального ассортимента продукции. Предприятие изготавливает два вида продукции — П1 и П2,которая поступает в оптовую продажу. Для производства продукции используются два вида сырья — А и В. Максимально возможные запасы сырья в сутки составляют 16 и 12 единиц соответственно. Расход сырья на единицу продукции вида П1 и вида П2дан в таблице 1. Опыт работы показал, что суточный спрос на продукцию П1никогда не превышает спроса на продукцию П2более чем на 2 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 4 д. е. — для П1 и 6 д. е. для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
Таблица 1
| Сырье | Расход сырья на 1 ед. продукции | Запас сырья, ед. | |
| П1 | П2 | ||
| А В |
Процесс построения математической модели для решения поставленной задачи начинается с ответов на следующие вопросы.
1. Для определения каких величин должна быть построена модель, т. е. как идентифицировать переменные данной задачи?
2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?
3. В чем состоит цель задачи, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Для рассматриваемой задачи ответы на эти вопросы сформулируем так: предприятию требуется определить объемы производства каждого вида продукции в тоннах, максимизирующие доход в д. е. от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов.
Для построения математической модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.
Предположим, что предприятие изготовит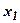 
единиц продукции П1 и 
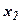единиц продукции П2. Поскольку производство продукции П1и П2 ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, должны выполняться следующие неравенства:
(ограничение запаса сырья А)
(ограничение запаса сырья В)
(ограничение соотношения спроса на П1 и П2)
(ограничение спроса на продукцию П2)
(условие неотрицательности объемов производства П1 и Р2)
Доход от реализации 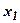единиц продукции П1 и 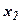единиц продукции П2 составит 
(целевая функция задачи). Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.
Поиск по сайту: