АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение задачи об ассортименте продукции графическим методом

Читайте также:
  1. B) Компенсация непредвиденных затрат в процессе производства продукции.
  2. D) объемы выпускаемых важнейших видов продукции
  3. D) постоянных затрат к разнице между ценой реализации продукции и удельными переменными затратами.
  4. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  5. I Психологические принципы, задачи и функции социальной работы
  6. I. 1.1. Пример разработки модели задачи технического контроля
  7. I. 1.2. Общая постановка задачи линейного программирования
  8. I. 2.1. Графический метод решения задачи ЛП
  9. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  10. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  11. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  12. I. Решение логических задач средствами алгебры логики

Рассмотрим решение задачи об ассортименте продукции графическим методом. Математическая постановка имеет следующий вид: целевая функция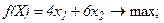

ограничения: (8)

(9)

(10)

(11)

(12)

Построим многоугольник решений (рис. 1). Для этого в системе координат на плоскости изобразим граничные прямые:

- (L1); - (L2);

- (L3); - (L4).

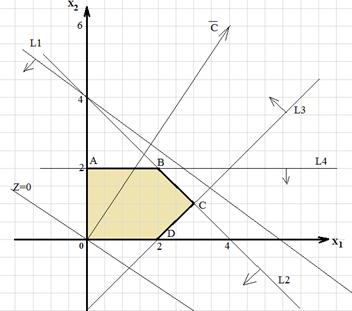
Рис. 1. Решение ЗЛП графическим методом

Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис. 1 показаны стрелками. Областью решений является многоугольник OABCD.

Для построения прямой строим вектор-градиент 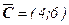и через точку О=(0;0) проводим прямую, перпендикулярную ему. Построенную прямую f(X) =0 перемещаем параллельно самой себе в направлении вектора . Из рис. 1 следует, что в точке В функция принимает максимальное значение. Точка В лежит на пересечении прямых L4 и L2.Для определения ее координат решим систему уравнений:

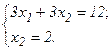
Оптимальное решение задачи 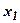= 2, 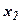=2. Подставляя значения 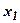и 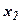в целевую функцию, получим: f(X) =4*2 + 6*2=20. Полученное решение означает, что объем производства продукции П1должен быть равен 2 ед., продукции П2 — 2 ед. Доход, получаемый в этом случае, составит: f(X) =20 д. е.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)