Задача 3. Определение пределов изменения коэффициентов целевой функции

Изменение коэффициентов целевой функции оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат. Вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того или иного ресурса. При анализе модели на чувствительность рассмотрение коэффициентов целевой функции необходимо дополнить исследованием следующих вопросов:

1) каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?

2) на сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным, и, наоборот, дефицитный ресурс сделать недефицитным?

Ответим на поставленные вопросы на нашем примере.Рассматривая первый вопрос, обозначим через и доходы предприятия от продажи единицы продукции П1 и П2 соответственно. Тогда целевую функцию можно представить в следующем виде

На рис. 1 видно, что при увеличении или уменьшении прямая, представляющая целевую функцию f(X), вращается (вокруг точки В)по часовой стрелке. Если же уменьшается или увеличивается, эта прямая вращается в противоположном направлении — против часовой стрелки. Таким образом, точка В будет оставаться оптимальной точкой до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых для ограничений (9) и (11).

Когда наклон прямой f(X) станет равным наклону прямой L2,получим две альтернативные оптимальные угловые точки - С и В. Аналогично, если наклон прямой f(X) станет равным наклону прямой для ограничения (11), будем иметь альтернативные оптимальные угловые точки А и В. Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение f(X) может достигаться при различных значениях переменных 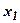и 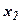. Как только наклон прямой выйдет за пределы указанного выше интервала , получим некоторое новое оптимальное решение.

Выясним, каким образом можно найти допустимый интервал изменения , при котором точка В остается оптимальной. Исходное значение коэффициента оставим неизменным. На рис. 1 видно, что значение можно уменьшать до тех пор, пока прямая f(X) совпадет с прямой L4 (отрезок АВ).

Это крайнее минимальное значение коэффициента можно определить из равенства углов наклонов прямой f(X) и прямой L4. Так как тангенс угла наклона для прямой f(X) равен , а для прямой (4) равен , то минимальное значение определим из равенства 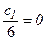, откуда min . На рис 1 видно, что значение можно увеличивать беспредельно, так как прямая f(X) при и не совпадает с прямой L2 (отрезок ВС и, следовательно, точка В при всех значениях коэффициента будет единственной оптимальной.

Интервал изменения , в котором точка В по-прежнему остается единственной оптимальной точкой, определяется неравенством . При оптимальными угловыми точками будут как точка В, так и точка А. Как только коэффициент становится меньше , оптимум смещается в точку А.

Можно заметить, что, как только коэффициент оказывается меньше , ресурс (9) становится недефицитным, а ресурс (11) - дефицитным. Для предприятия это означает следующее: если доход от продажи единицы продукции П1 станет меньше д.е. (а меньше быть не может), то наиболее выгодная производственная программа предприятия должна предусматривать выпуск максимально допустимого количества продукции П2(полностью удовлетворять спрос на продукцию П2).При этом соотношение спроса на продукцию П1 и П2 не будет лимитировать объемы производства, что обусловит не дефицитность ресурса (8). Увеличение коэффициента свыше д. е. не снимает проблему дефицита ресурса (8). Точка В — точка пересечения прямых L2 и L4 - остается все время оптимальной.

Поиск по сайту: