 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ЗАДАЧА О НАЗНАЧЕНИЯХ
В процессе управления производством зачастую возникают задачи назначения исполнителей на различные виды работ, например, подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами научно-технического развития и т.п.. Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Любой рабочий может выполнить только одну работу. Требуется так распределить работы между рабочими, чтобы общие затраты на выполнение всех работ были минимальными.
Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ.
Введем обозначения:
сij — показатель эффективности назначения i -го рабочего на j -ю работу, например, издержки выполнения i- м рабочим j -й работы;
xij — переменная модели (хij = 1, если i -й рабочий используется на j -й работе, и xij = 0 в противном случае).
Математическаямодель задачи о назначениях:
(13)
(14а)
(14б)
(15)
Здесь (13) - целевая функция (минимум издержек на выполнение всех работ); (14) – система ограничений, отражающая следующие условия: а) – каждый рабочий может быть привлечен к одной работе; б) – каждая работа должна быть выполнена одним рабочим; (15) – условия двоичности переменных.
При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={ сij }, элементами которой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов.
Результатом решения задачи о назначениях (13) – (15) является вектор х * = { 
}, компоненты которого – целые числа. Решение задачи о назначениях (13) – (15) можно представить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна 1. Такую матрицу также называют матрицей перестановок. Значение целевой функции (13), соответствующее оптимальному назначению, называют эффективностью назначений.
В комбинаторной интерпретации задача о назначениях заключается в определении такой перестановки исполнителей {1,2,…, n }, которая обеспечивает минимальную суммарную стоимость назначений. Очевидно, что решение такой задачи может быть получено перебором, однако существует ряд эффективных алгоритмов.
При решении задачи о назначениях в OpenOffice.orgCalc используются возможности самой программы – инструмент для поиска решений уравнений и задач оптимизации.
Следующая последовательность шагов описывает процесс решения задачи о назначениях в OpenOffice.orgCalc.
Шаг 1. Открываем электронную таблицу OpenOffice.orgCalc. Вводим в некоторый диапазон ячеек матрицу весов заданную в условии задачи (рис.4). Делаем необходимые подписи.
Шаг 2. Заполняем диапазон ячеек единицами, равный по размеру заданной матрице весов, но расположенный таким образом, чтобы он не перекрывал матрицу весов. Эта матрица назначений (переменные задачи), предварительно заполненная единицами. Расставляем необходимые подписи.
Шаг 3. Вычисляем значение целевой функции (13) и помещаем его в некоторую ячейку. Целевая функция равна сумме произведений значений из диапазона, заданного в шаге 1 и диапазона, заданного в шаге 2. Для этого вызываем мастер функций соответствующей кнопкой (или из меню Функции\Вставить функцию) и выбираем функцию SUMPRODUCT. В полях «Массив 1» вводим диапазон ячеек из шага 1, делая на них ссылку, а в «Массив 2» вводим диапазон из шага 2. Нажимаем кнопку «ОК» (рис. 4).
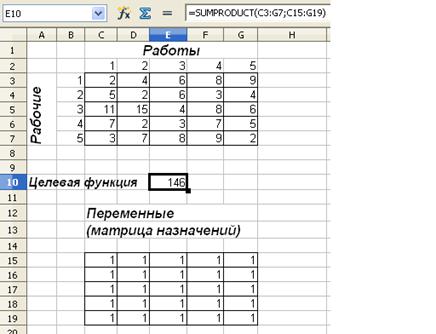
Рис. 4. Ввод матрица весов, переменных и вычисление
целевой функции
Шаг 4. Вводим левые части ограничений (14а)-(14б). Для этого выполняем суммирование значений элементов первого столбца матрицы, полученной в шаге 2, и размещаем результат, например, под первым столбцом матрицы весов. Заполняем с помощью операции автозаполнения ячейки под всеми остальными столбцами матрицы весов.
Выполняем суммирование значений элементов первой строки матрицы, полученной в шаге 2, и размещаем результат, например, за последним элементом первой строки матрицы весов. Заполняем с помощью операции автозаполнения ячейки за всеми остальными строками матрицы весов (рис. 5).
Рис. 5. Добавление ограничений
Шаг 5. Выполняем команду Сервис\Решатель…. На экране появится окно, представленное на рис. 6. Необходимо заполнить следующие данные:
1) в поле «Целевая ячейка» даем ссылку на ячейку из шага 3, т.е. ячейку, в которой вычисляется значение целевой функции;
2) установить точку на переключателе «Минимум»;
3) в поле «Изменяя ячейки» даем ссылку на диапазон ячеек таблицы из шага 2 (матрицы назначений).
4) ввести ограничения задачи (2) – (4) в поле «Ограничительные условия». Вводим 3 группы ограничений, как показано на рис. 6.
Рис. 6. Окно «Решатель…»
5) Нажимаем «Решить». После чего в матрице назначений будет представлено решение задачи, а в целевой ячейке будет показано значение целевой функции, соответствующее оптимальному назначению (рис.7).
Рис. 7. Результат
Поиск по сайту: