Законы реляционной алгебры

Оптимизация SQL-запросов

Последовательность оптимизации запросов и используемые законы реляционной алгебры

Основные шаги оптимизации

Поступающий на сервер SQL-запрос подвергается оптимизации с целью уменьшения времени его выполнения. При этом оптимизатор запросов выполняет следующие шаги:

I. Строит логический план выполнения запроса (дерево логических операций).

II. Строит оптимальный физический план выполнения запроса (дерево физических операций).

III. Реализует полученный оптимальный физический план выполнения запроса.

Примечание. Оптимизатор называется восходящим, если при построении оптимального физического плана он просматривает логический план от листьев к корню. Если логический план просматривается от корня к листьям, то такой оптимизатор называется нисходящим.

Законы реляционной алгебры

Для построения логического плана выполнения запроса используются законы реляционной алгебры, некоторые из которых рассмотрены ниже.

1.Закон коммутативности декартова произведения.

Имеет место равенство:

R₁ × R₂ = R₂ × R₁ ,

где R₁ и R₂ – отношения (таблицы).

2. Закон ассоциативности декартова произведения.

Справедливо равенство:

(R₁ × R₂) × R₃ = R₁ × (R₂ × R₃),

где R₁, R₂ и R₃ – отношения (таблицы).

3. Закон каскада проекций.

Если , где {a₁, …, a_n} и {b₁, …, b_m} – некоторые множества атрибутов, то имеет место следующее равенство:

.

4. Закон каскада селекций.

Если условие F является конъюнкцией нескольких условий, т.е. , то справедливо следующее равенство:

.

5. Закон перестановки проекции и селекции:

1. В условие F входят атрибуты только из множества {a₁, …, a_n}.

Имеет место следующее равенство:

.

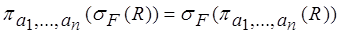2. В условие F входят атрибуты не только из множества {a₁, …, a_n}.

Справежливо следующее равенство:

,

где b₁, …, b_m – атрибуты таблицы R, которые входят в условие F, но не принадлежат множеству {a₁, …, a_n}.

6. Закон перестановки селекции и декартова произведения.

Если условие f₁ включает в себя только атрибуты отношения R₁, то имеет место следующее равенство:

.

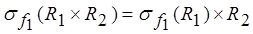Следствие. Пусть , причем в f₁ входят атрибуты только из отношения R₁, а в f₂ входят атрибуты только из R₂. В этом случае справедливо следующее равенство:

.

7. Закон перестановки селекции и объединения.

Имеет место следующее равенство:

.

Примечание. В языке SQL операция объединения отношений моделируется с помощью операции UNION.

8. Закон перестановки селекции и разности отношений.

Справедливо следующее равенство:

,

где R₁ – R₂ – множество кортежей, которые принадлежат отношению R₁ и не принадлежат R₂.

9. Закон перестановки проекции и декартова произведения.

Пусть {b₁, …, b_n} – некоторые атрибуты из R₁, {с₁, …, с_m} – некоторые атрибуты из R₂. Имеет место следующее равенство:

10. Закон перестановки проекции и объединения.

Справедливо следующее равенство:

.

1.2. Построение логического плана

При построении логического плана выполнения SQL-запроса выполняются следующие действия:

1. Запрос преобразуется в формулу реляционной алгебры (явно или неявно).

2. Выполняется преобразование (оптимизация) этой формулы.

Поиск по сайту: