АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Линейное программирование. Задача использования сырья. Обобщение задача использования сырья

Читайте также:
  1. I. 3.1. Двойственная задача линейного программирования
  2. II.2. Задача о назначениях
  3. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  4. VI. Общая задача чистого разума
  5. Анализ активов организации и оценка эффективности их использования.
  6. Анализ влияния изменения правых частей ограничений на значения целевой функции (чувствительность решения к изменению запасов сырья).
  7. Анализ влияния использования прибыли на финансовое положение предприятия
  8. Анализ влияния факторов на повышение эффективности использования основных средств
  9. Анализ влияния эффективности использования материальных ресурсов на величину материальных затрат
  10. Анализ доходности и эффективности использования собственного капитала
  11. Анализ и оценка влияния на объем продаж использования производственных ресурсов.
  12. Анализ использования капитала

Линейное программирование – это наука о методах исследования и отыскания наибольшего и наименьшего значений линейной функции на неизвестные которой наложены линейные ограничения.

Задача линейного программирования относится к задачам на условный экстремум функции, но применить хорошо разработанные методы математического анализа невозможно.

Пусть необходимо исследовать на экстремум линейную функцию Z.

Z= при линейных ограничениях:

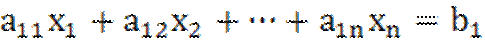
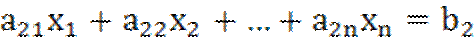
Так как Z- линейная функция, то = (j=1,n)

Но все коэффициенты линейной функции не может быть = 0, следовательно внутри области, образованный системой ограничений, экстремальные точки . Они могут быть на границе области, но исследовать точки экстремума невозможно, так как частные производные являются константами.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)