АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема 2 ( о замкнутом, ограниченном, выпуклом многограннике)

Читайте также:
  1. I. 4.1. Первая теорема двойственности
  2. S-M-N-теорема, приклади її використання
  3. Б1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
  4. Базисный минор и ранг матрицы. Теорема о базисном миноре
  5. Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
  6. Билет 5 Теорема Безу и следствия из неё. Основная теорема алгебры.
  7. Внешние эффекты (экстерналии). Теорема Коуза.
  8. Внешние эффекты и внешние затраты. Государственная политика в случаях их возникновения. Теорема Коуза.
  9. Внешние эффекты трансакционные издержки. Теорема Коуза
  10. Внешние эффекты, их виды и последствия. Теорема Коуза
  11. Внешние эффекты. Теорема Коуза.
  12. Внешние эффекты. Теорема Коуза.

Th. Замкнутый ограниченный выпуклый многогранник является выпуклым множеством комбинаций своих угловых точек.

Док-во: Рассмотрим многоугольник имеющий n вершин. Докажем, что для любая точка треугольника удовлетворяет теореме 2.

А1 А2

 

 

А4

 

А3

 

В ∆ А1А2А3 возьмем производную точку А и через нее проведем отрезок . Так как А€ , то она выпуклая линейная комбинация ее концов

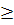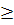А4=λ1А1+ λ4А4, где λ1 0, λ4 0

λ1+ λ4=1 (1)

Точка А4€ точка А4-выпуклая линейная комбинация ее концов.

А4=λ2А2+ λ3А3 +…+ λ2+λ3 =1 (2)

Представляем (2) в (1)

Получаем: А= λ1А1+ λ4(λ2А2+ λ3А3)= λ1А1+ λ4λ2А2+ λ4λ3А3

λ1=t1; λ4 λ2= t2; λ4 λ3= t3;

А= t1А1+ t2А2+ t3А3; t1+ t2+ t3=1; t1≥0; t2≥0; t3≥0

Т.е А является выпуклой линейной комбинацией точек. Рассмотрим многоугольник, имеющий n>3 вершин. С помощью диагонали разобьем многоугольник n-2 ∆ тогда точка А попадает в 1 из треугольников для определенности возьмем ∆ А1А2А3

А= λ1А1+ λ2А2+ λ3А3; λ1+ λ2+ λ3=1

Добавим остальные вершины умноженные на нуль

А= λ1А1+ λ2А2+ λ3А3+0А4+…+Аn

То есть точка А выпуклая линейная комбинация угловых точек множества.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)