Теорема 3

Множество всех планов задачи линейного программирования выпукло.

Док-во. Докажем, что если x1и x2планы задачи линейного программирования a1x1+a2x2+…+anxn≤b (1); a1x1+a2x2+…+anxn+x n+1=b (2), то их выпуклая линейная комбинация x=λ1x1+ λ2x2, λ1≥0, λ2≥0, λ1+ λ2=1явл-ся планом задачи лин. программирования.

Т.к. x1и x2планы задачи, то выполняются соотношения:

Ax1=A0, x1≥0

Ax2=A0, x2≥0, тогда Ax=A(λ1x1+ λ2x2) =Aλ1x1+ Aλ2x2=λ1A0 + λ2A0= A0(λ1+ λ2)=A0 => что план x удовлетворяет соотнош. (2) т.к. λ1≥0, λ2≥0, x1, x2≥0 => x-план задачи линейного программирования. Ч.т.д.

9)Теорема 4(о достижении минимального значения в угловой точке).Примечание: здесь L=лямбда.

Линейная функция задачи линейного программирования достигает min значения в угловой точке многовариантного решения.Если линейные функции задачи линейного программирования принимают min значение более чем в одной угловой точке, то она достигает того же значения в любой точке, является выпуклой линейной комбинацией этих точек.

Докозательство:Пусть оптимальный план X0-не является угловой точкой.Тогда по Теореме 2 X0 можно представить X0=L1X1+…+LpXp;

Li>=(i=1,p); ∑^p_i=0Li=1;

Так как Z(x)-линейная функция, получаем Z(X0)=Z(L1X1+….+LpXp)=L1Z(X1)+L2Z(X2)+…..+LpZ(Xp) (1)

Среди Z(Xi) (i=1,p) выберим наименьшее значение. Оно соответствует угловой точке Xk, (k=1,p) и обозначим его через m, т.е Z(Xk)=m.

Заменим в уравнение (1) каждое значение Z(Xi) этим наименьшим значением Z(X0)>=L1m+L2M+….+Lpm=m∑^p_i=0Li=m;

По предложению X0 -оптимальный план; поэтому Z(X0)<=m, но по даказательству Z(X0) >=m и Z(X0)=m=Z(Xn); где Xn-угловая точка.

Итак, существует угловая точка в которой линейная линейная функция принимает min значение.

Для доказательства 2-ой части допустим, что Z(x) принимает min значение более чем в одной угловой точке.

Example:

X1,X2,….,Xq (q=1,p)

Тогда Z(X1) =Z(X2)=….=Z(Xq)=m

Если X-выпуклая линейная комбинация этих точек

X=L1X1+….+LqXq, то Z(x)=Z(L1X1,+…..+LqXq)=L1Z(X1)+…..+LqZ(Xq)=L1m+….+Lqm= m(∑^p_i=0Li)=m;

Т.е линейная функция Zàmin в любой точке X, являющаяся выпуклой линейной комбинацией угловых точек.

10. Построение опорного плана

Пусть необходимо решить задачу:

,

Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:

где x_n+i ≥ 0, i=1,...,p.

В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:

Правила выбора разрешающего элемента при поиске опорного плана.

1.При условии отсутствия "0-строк" (ограничений-равенств) и "свободных" переменных (т.е. переменных, на которые не наложено требование неотрицательности).

• Если в столбце свободных членов симплексной таблицы нет отрицательных элементов, то опорный план найден.
• Есть отрицательные элементы в столбце свободных членов, например b_i<0. В такой строке ищем отрицательный коэффициент a_il, и этим самым определяем разрешающий столбец l. Если не найдем отрицательный a_il, то система ограничений несовместна (противоречива).
• В качестве разрешающей выбираем строку, которой соответствует минимальное отношение: , где r - номер разрешающей строки. Таким образом, a_rl - разрешающий элемент.
• После того, как разрешающий элемент найден, делаем шаг модифицированного жорданова исключения с направляющим элементом a_rl и переходим к следующей симплексной таблице.

2. В случае присутствия ограничений-равенств и "свободных" переменных поступают следующим образом.

• Выбирают разрешающий элемент в "0-строке" и делают шаг модифицированного жорданова исключения, после чего вычеркивают этот разрешающий столбец. Данную последовательность действий продолжают до тех пор, пока в симплексной таблице остается хотя бы одна "0-строка" (при этом таблица сокращается).
• Если же присутствуют и свободные переменные, то необходимо данные переменные сделать базисными. И после того, как свободная переменная станет базисной, в процессе определения разрешающего элемента при поиске опорного и оптимального планов данная строка не учитывается (но преобразуется).

11.12.Симплексный метод. Отыскание оптимального плана. Условие оптимальности. Теорема 5.

Каждой угловой точке многогранника решений соответствует опорный план. Каждый опорный план определяется системой m-линейно-независимых векторов.

Симплекс метод позволяет исходя из известного опорного плана перейти к оптимальному плану.

Пункт 1- построение опорных планов.

Найти минимальное значение линейной функции.

Z=C1X1+….+CnXn при ограничениях (1)

a11*X1+….a1n*Xn=b1

….. (2)

am1*X1+…anm*Xn=bm

Предположим, что система ограничений содержит m единичных первых векторов, т.е

X1+…+a1,m+1*Xm+1+…+am1*Xn=b1

X2+…+a2,m+1*Xm+1+…+am2*Xn=b2

Xm+…+am,m+1*Xm+1+…+amn*Xn=bm

Xj≥0 j=1.n

Запишем в векторном виде:

X1A1+X2A2+…+XnAn+Xm+1Am+1+…+XnAn=A0 (4)

Где А1=(1,0,…0), А1=(0,1,…0), Аm(0…1),

am+1= (a1,m+1 a2,+1 an, m+1)

A0=(b1,b2…bm)

А1,А2…Аm- Линейно-независимые векторы m-мерного пространства, они образуют базис пространства, поэтому в разложении (4) за базисное неизвестное выбираем Х1,Х2…Хn, свободные неизвестные приравниваем к нулю, учитывая bi ≥0, а вектор А1,А2,…,Am-единичный, получаем первоначальный план

Х0=(X1=b1, X2=b2,…,Xn=bn, Xnm=0, Xn=0) (5)

Плану (5) соответствует разложение

X1A1+…+XnAn=A0 (6)

Вектор А1, …,Аm-линейно-независимый план, следовательно план (5) – опорный.

Вектор А1, …,Аm образуют базис в m-мерном пространстве, поэтому каждый из n-векторов в соотношении (4) можно разложить по векторам базиса единственным образом.

Aj= Ai

Предположим, что для некоторого вектора, не входящего в базис, например, для вектора Аm+1 положителен хотя бы 1 из коэффициентов Xi,m+1 в разложении (7)

Х1, m+1*A1+ Х2, m+1*A2+…+Xm,m+1Am=Am+1 (7)

Зададим некоторое число θ>0 (пока неизвестно) умножим на него обе части равенства (7) и вычтем результат почленно из равенства (6)

Получаем:

(X1-θX1,m+1)A1+(X2-θX2,m+1)A2+…+(Xm-θXm,m+1)Am+θAm+1=A0 (8)

X1=(X1-θX1,m+1;……; Xm-θXm,m+1; θ; 0,….0)

Вектор Х1 является планом задач, если все его компоненты неотрицательны, следовательно необходимо найти θ чтобы (Хi-θXi,m+1)≥0

Получаем θ≤ следовательно вектор Х1- план задачи для любого θ удовлетворяет условие:

0<θ<min 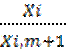(10)

Где min берется по I для которого Xi,m+1>0

Опорный план не может содержать m+1положительный компонент, поэтому компонент, поэтому в плане Х1 необходимо обнулить по кратней мере 1 компоненту.

Пусть в (10) θ= θ0=min (11)

Компонента, для которой достигается min обращается в 0.

Для определения опорного плана необходимо любой вектор не входящий в базис А2, А3,…Аm, Am+1 разложить по векторам этого базиса. После определить такое θ0>0 при котором исключался бы 1 из векторов этого базиса.

Поиск по сайту: