 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обобщенная задача использования сырья
Пусть при выпуске n видов продукции используют m видов сырья.
Обозначим через  - виды сырья (i=1,n)
- виды сырья (i=1,n)
 -запасы сырья i-го вида
-запасы сырья i-го вида
 -виды продукции (j=1,n)
-виды продукции (j=1,n)
 - количество ед. i-го сырья, идущего на изготовление j-той продукции
- количество ед. i-го сырья, идущего на изготовление j-той продукции
 - величина прибыли,получаемая от реализации единицы j-той продукции.
- величина прибыли,получаемая от реализации единицы j-той продукции.
Пусть  -Количество j-той продукции, которую нужно произвести. Такая математическая модель задачи имеет вид:
-Количество j-той продукции, которую нужно произвести. Такая математическая модель задачи имеет вид:
| Виды сырья | Запасы сырья | Количество ед. i-го сырья на изготовление ед. j-той продукции | |||

| 
| 
| 
| ||

| 
| 
| 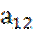
| 
| 
|

| 
| 
| 
| 
| 
|
| |||||
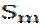
| 
| 
| 
| 
| 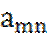
|
| Прибыль от ед. продукции | 
| 
| 
| 
|
Z=  +
+  +
+  +
+ 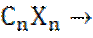 max
max
 +
+  +
+  +
+ 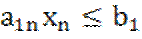
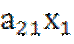 +
+ 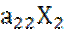 +
+  +
+ 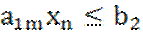
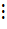
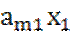 +
+ 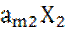 +
+  +
+  ,
,

 (j=1,n)
(j=1,n)
 (i=1.m)
(i=1.m)
Поиск по сайту: