Несимметричные двойственные задачи

Теорема двойственности:

Система ограничений исходной задачи в несимметричных двойственных задачах определяется как равенство. Двойственная же задача задается, как неравенство, причем переменные могут быть и отрицательными. Что бы проще понимать постановку задачи будем интерпретировать ее в матричной форме.

Теорема 2. Для пары двойственных задач имеет место соотношение

.

Доказательство.

Мы докажем эту теорему только для несимметричной пары двойственных задач, причем это доказательство не является строгим.

Итак, рассмотрим исходную задачу линейного программирования

Представим себе, что мы решаем эту задачу при помощи симплекс-метода. Рассмотрим окончательный вид симплекс-таблицы. Не теряя общности, можно считать, что в окончательный базис вошли векторы (в конце концов, векторы всегда можно перенумеровать). Тогда окончательная симплекс-таблица имеет вид

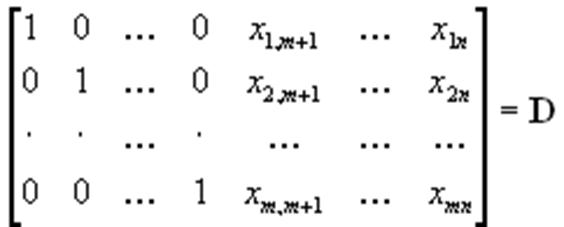
и оптимальный план имеет вид .

Обозначим через

вектор и черезB матрицу

,

то есть  матрица, составленная из базисных векторов .

Так как

, то для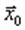

мы получаем уравнение

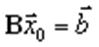, откуда .

матрица,то легко догадаться, что ,

откуда .

Пусть  вектор коэффициентов целевой функции и . Пусть далее  векторы, соответствующие

столбцам матрицы 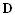. Вспоминая выражения для

легко получить, что

,

то есть для всех j верно неравенство . В векторной форме это выглядит так

.

Получив основные соотношения для оптимального плана исходной задачи, перейдем теперь к двойственной задачею Для этого рассмотрим вектор , определяемый соотношением

.

Для него мы имеем:

,

то есть вектор удовлетворяет ограничениям двойственной задачи. Но для него

.

В силу следствия 2 теоремы 1 является оптимальным планом двойственной задачи, а так как выполнено соотношение , то это и означает, что

.

Теорема доказана.

Блок 1

1)Линейное программирование.Задача использования сырья.Обобщение задачи использования сырья.

2)Задача составления рациона.Обобщение задачи составления рациона.

3)Замена неравенства уравнениями.Теорема 1

4)Переход к равенствам в задаче использования сырья и задачи составления рациона.

5)Общая задача линейного программирования.Три формы записи.определения.

6)Выпуклые множества.Определения.

7)Теорема 2

8)Теорема 3

9)Теорема 4

10)Симплексный метод.построение опорных планов.

11) Симплексный метод.Отыскание оптимального плана.Условие оптимальности.Теорема 5

12) Симплексный метод.Отыскание оптимального плана.Условие оптимальности.Теорема 6

13)Симплексный метод.Метод исскуственного базиса.Теорема.

14) Симплексный метод.Задача со смешанными ограничениями.

15)Двойственность в линейном программировании.Несимметричные двойственные задачи.Теорема.

Блок2

1)Вариационное исчисление.введение.Задача о брахистохроне.

2)Простейшая задача вариационного исчисления.Определения.

3)Необходимые условия слабого локального минимума.Теорема.

4)Основная лемма вариационного исчисления.Лемма Ланранжа.Уравнение Эйлера.Теорема.

5)Лемма Дюбуа-Реймонда.Примеры Гильберта и Вайерштрасса.

6)Задача Больца.Теорема 1

7)Необходимые условия Вейерштрасса.Теорема 2

8)Условие Лежандра.Теорема 1

9)Условие Якоби.Теорема 2

10)Функционалы зависящие от n неизвестных функций.Теорема 3

11) Функционалы зависящие от производных высших порядков.Теорема 4

12)Изопереметрическая задача. Теорема 1

13) Изопереметрическая задача в общем случае(от n переменных) Теорема 2.

14)Условный экстремум.Задача Лагранжа.Теорема 3.

15)Обобщение задача на условный экстремум.Функционал Лагранжа.Теорема4.

Поиск по сайту: