Регрессионный анализ

Регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:

где у - зависимая переменная (она всегда одна);

х_i - независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п 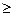2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

· построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x ₁, x ₂, …, x_n.

· оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный - одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x _l ,x ₂ ,...,x_n; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида:

Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

где т - число наблюдений;

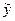^j = a + b ₁ x ₁ ^j + b ₂ x ₂ ^j+... + b_nх_n^j - расчетное значение результатного фактора.

Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для персонального компьютера или специального финансового калькулятора. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти по формулам:

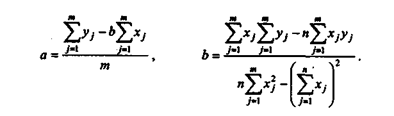
Рассмотрим использование методов корреляционного и регрессионного анализа на примере 2.13.

Пример 2.13. Наибольшим спросом в торговых точках города, реализующих молочную продукцию, пользуется молоко "Лето", выпускаемое в пакетах объемом 1 литр. Цены за единицу этого товара в разных торговых точках города варьируют.

Известно, что реализация этого продукта вносит существенный вклад в общую выручку торговых точек. Возможно, она влияет и на величину прибыли предприятий торговли. Так ли это - позволит установить анализ.

1. По данным, касающимся цен на упаковку молока "Лето" и объемов реализации в 15 торговых точках города, построим уравнение регрессионной зависимости между этими факторами.

2. Методом регрессионного анализа определим, есть ли связь между величиной чистой прибыли предприятий торговли и объемами реализации ими молока "Лето", если для всех 15 анализируемых точек известны величины прибыли за II квартал 1999 г., а также цены и объемы реализации данной марки молока (табл. 2.5).

Таблица 2.5

Показатели деятельности торговых предприятий, реализующих молоко "Лето", за II квартал 1999 г.

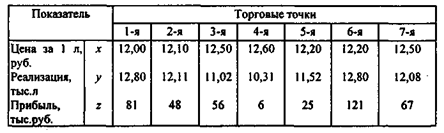
Анализ будем проводить с помощью табличного процессора MS Excel. Описательная статистика для представленных данных отражена в табл. 2.6.

Таблица 2.6

Описательная статистика реализации молока "Лето" торговыми точками

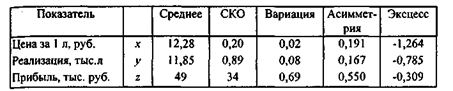
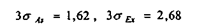
1. Анализ следует начать с проверки однородности совокупности данных. Критерием однородности является условие:

Var < 0,33.

Видим, что это условие выполняется лишь для рядов данных, относящихся к ценам (фактор x) и объемам реализации (фактор у) молока.

Проверка нормальности распределений этих факторов показывает:

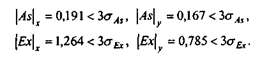
Условия нормальности выполняются, следовательно, по двум этим рядам данных можно строить регрессионную зависимость.

Следующим шагом при построении регрессионной модели будет определение результативного и факторного признаков. Исходя из сути поставленной задачи, можно сказать, что в данном случае независимым фактором является цена за литр, объем реализации - признак зависимый (результатный).

Регрессионная зависимость между факторами х и у (зависимость объема реализации молока от его цены) будет иметь вид:

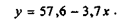
Полученный результат - обратно пропорциональная зависимость между факторами - вполне согласуется со здравым смыслом: очевидно, что чем выше цена, тем менее привлекательна торговая точка для покупателей данного товара.

Регрессионная зависимость позволяет строить прогноз величины результативного фактора при известной величине зависимого (т.е. прогноз объема реализации от цены за литр молока).

Подставив, например, х = 12,40 руб. за литр в аналитическую формулу зависимости, получим ожидаемое значение объема реализации за квартал - y = 11,72 тыс. литров.

2. Определить, связан ли объем прибыли, полученной предприятиями торговли, с объемами реализации ими одного вида продукции, можно с помощью корреляционного анализа. Матрица корреляций, рассчитанная с помощью компьютера, выглядит так:

Величины коэффициентов парной корреляции факторов таковы:

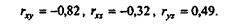
Эти величины свидетельствуют о том, что между ценой товара (х) и объемом его реализации (у) связь весьма тесная (величина 0,82 говорит о том, что 82% вариации фактора у объясняются вариацией фактора х). Прибыль предприятия от цены на этот товар зависит слабо (коэффициент корреляции равен -0,32), а вот связь величины прибыли и объемов реализации молока "Лето" оказалась средней силы (r_yz = 0,49), причем зависимость прямо пропорциональная.

Следовательно, увеличение объемов реализации этого товара в среднем довольно заметно влияет на рост прибыли предприятий торговли. По результатам анализа руководству магазинов следует подумать о мерах по стимулированию продажи молока этой марки.

Можно ли построить и регрессионную зависимость прибыли от исследуемых факторов?

Для полного ряда из 15 значений критерий однородности (Vаr < 0,33) не выполняется, следовательно, использовать полный ряд значений прибыли нельзя. Лишь исключив по четыре наибольших и наименьших значения, можно привести этот ряд к однородности. Проверка нормальности для усеченной совокупности данных (по 7 оставшимся магазинам) показывает, что все три ряда значений нормальны. Правда, при этом вызывает сомнение правомочность использования статистических процедур на столь малой выборке. Однако если отвлечься от этого факта, то и в этом случае зависимость вида z = а + b ₁ х + b ₂ у не даст аналитику значимой информации, поскольку между факторами х и у наблюдается сильная взаимозависимость (мультиколлинеарность) - об этом свидетельствует высокое значение парного коэффициента корреляции (на усеченной выборке r_xy = -0,88).

Поэтому при регрессионном анализе прибыли целесообразно брать лишь один из этих факторов, а именно объем реализации, поскольку его связь с величиной прибыли более тесная (r_yz = 0,78, тогда как r_xz = 0,48 - также по усеченной выборке).

Необходимо отметить, что в экономических исследованиях корреляционный и регрессионный анализы нередко объединяются в один - корреляционно-регрессионный анализ. Подразумевается, что в результате такого анализа будет построена регрессионная зависимость (т.е. проведен регрессионный анализ) и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ). В известном смысле корреляционная связь носит более общий характер, поскольку она не предполагает наличия зависимости "причина - следствие".

Поиск по сайту: