Приемы цепных подстановок и арифметических разниц

Метод цепных подстановок еще называют приемом последовательного (постепенного) изолирования факторов. Этот метод предназначен для измерения влияния изменения факторных признаков на изменение результативного показателя при изучении функциональных зависимостей. Правомерность применения метода обосновал К. Маркс при изучении влияния на относительную цену рабочей силы трех факторов: продолжительности, производительной силы и интенсивности труда. Он предложил последовательно рассматривать каждый фактор как переменный, фиксируя все остальные, - и так по очереди.

Общую схему приема цепных подстановок рассмотрим на примере трехфакторной мультипликативной модели:

где T - результатный показатель; а, b, с - факторные показатели.

Сравним фактические значения показателей (индекс "ф") с плановыми (индекс "п"). Полное отклонение показателя Т от плана составит:

Часть полного отклонения, обусловленная вариацией каждого из факторов, имеет вид:

Таким образом:

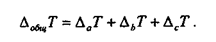
Прием цепных подстановок может быть использован при анализе отклонений фактических значений экономических показателей от плановых, а также при изучении динамики показателей.

Естественным следствием приема цепных подстановок является прием арифметических разниц.

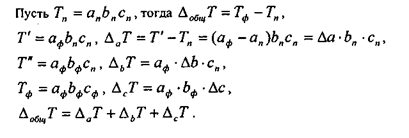
Приемы цепных подстановок и арифметических разниц - достаточно простые и универсальные аналитические приемы. Однако они не инвариантны относительно порядка замены факторов. От того, в какой последовательности происходит замена, будет зависеть результат разложения.

Существенным недостатком этих методов является также и то, что они обладают свойством неаддитивности по времени. Это означает, что результаты анализа, выполненного, например, за целый год, не будут совпадать с суммой соответствующих данных, полученных по месяцам или кварталам.

Проиллюстрируем важность порядка замены факторов при применении приема цепных подстановок для анализа товарооборота торгового предприятия за месяц на примере 2.2.

Пример 2.2. Имеются данные о численности работающих (Ч) на торговом предприятии и выручке на одного работающего (В) за сентябрь. Сравним плановые и фактические значения показателя товарооборота (Т).

Рассмотрим две модели, различающиеся порядком факторов.

Результаты получились разные. Это показывает, что порядок замены в мультипликативной модели крайне важен для интерпретации полученных результатов.

Метод арифметических разниц нецелесообразно использовать для кратных моделей. Покажем это на примере 2.3.

Пример 2.3. Рассмотрим плановые и фактические значения показателя фондовооруженности предприятия (Ф). Этот показатель исчисляется как частное от деления среднегодовой величины основных фондов предприятия (S) на среднегодовую численность работающих (Ч).

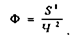
Используя прием цепных подстановок, запишем:

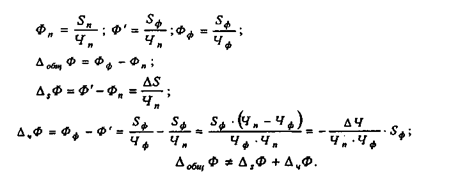
Если бы мы слепо следовали приему арифметических разностей, следовало бы написать:

Таким образом, прием арифметических разниц для кратных моделей использовать нельзя.

Поиск по сайту: