Метод сценариев

Еще один вариант использования ситуационного анализа для прогнозирования возможных действий имеет более общее применение. Теоретически существует три типа ситуаций, в которых необходимо проводить анализ и принимать управленческие решения, в том числе и на уровне коммерческой организации: в условиях определенности, риска (неопределенности) и конфликта. Однако с позиции прогнозирования вариантов возможных действий наибольший интерес представляет алгоритмизация действий в условиях неопределенности.

Эта ситуация встречается на практике достаточно часто. Здесь применяется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им вероятностей, т.е. разработка определенных сценариев развития событий. При этом используются: а) известные, типовые ситуации (типа: вероятность появления герба при бросании монеты равна 0,5); б) предыдущие распределения вероятностей (например, из выборочных обследований или статистики предшествующих периодов известна вероятность появления бракованной детали); в) субъективные оценки, сделанные аналитиком самостоятельно либо с привлечением группы экспертов.

Таким образом, последовательность действий аналитика при проведении анализа ситуации в условиях неопределенности такова:

• прогнозируются возможные исходы R_k, k = 1,2,.... n; в качестве R могут выступать различные показатели, например, доход, прибыль, приведенная стоимость ожидаемых поступлений и др.;

• каждому исходу присваивается соответствующая вероятность R_k, причем

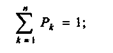
• выбирается критерий (например, максимизация математического ожидания прибыли):

• выбирается вариант, удовлетворяющий выбранному критерию.

Простейшую иллюстрацию метода сценариев представляет пример 2.1.

Пример 2.1. Имеются два объекта инвестирования с одинаковой прогнозной суммой требуемых капитальных вложений. Величина планируемого дохода (тыс. руб.) в каждом случае неопределенна и приведена в виде распределения вероятностей:

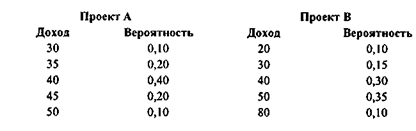
Тогда значения математического ожидания дохода для рассматриваемых проектов будут соответственно равны:

Е (R_A) = 30 ∙ 0,10 + 35 ∙ 0,20 + 40 ∙ 0,40 + 45 ∙ 0,20 + 50 ∙ 0,10 = 40 тыс. руб.

Е (R_B) = 44 тыс. руб.

Таким образом, по критерию дохода проект В следует признать более предпочтительным. Необходимо, правда, отметить, что этот проект является и относительно более рисковым, поскольку имеет большую вариацию дохода по сравнению с проектом А.

В данном случае единственным критерием отбора варианта была максимизация математического ожидания дохода. В более сложных ситуациях в анализе используют так называемый метод построения дерева решений (см. раздел 2.9.1).

Поиск по сайту: