Метод квадратичной интерполяции – экстраполяции

Данный метод относится к классу прямых методов, опирающихся на идею построения аппроксимирующего полинома второго порядка на основании информации о значениях функции в n+1 точке – узлах интерполяции.

Начальный этап

1. Выбрать произвольную точку x¹ÎRⁿ

2. Задаться величиной шага h=0.001

3. Определить погрешность

4. Положить счётчик числа итераций равным 1, а также b=x¹

Основной этап

Шаг 1. Вычислить f_i в 3-х точках: a, b и с – центральной (b) и двух соседних: a=b-h, c=b+h. Затем, по формуле

(1)

или

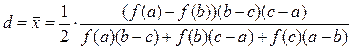(2)

найти аппроксимирующий минимум d

Шаг 2. Проверить критерий близости 2-х точек b и d

и

Если оба условия выполняются – фиксируем аппроксимирующий минимум

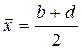
и останавливаемся. Если оба критерия не выполняются, полагаем b=d и возвращаемся на шаг 1.

Метод Пауэлла

Метод Пауэлла является одним из самых популярных методов. Эффективен как и рассмотренный ранее алгоритм квадратичной интерполяции – экстраполяции, если начальная точка x¹Îd(x*).

Начальный этап

1. Выбрать ε₁, ε₂, h.

2. Взять 3 точки a, b, c на равных на равных интервалах. Предполагается, что сработал метод Свенна и получен интервал [a, b].

a=a;

c=b;

b=(a+c)/2;

Основной этап

1. Найти аппроксимирующий минимум на 1-й итерации по формуле:

на последующих итерациях по формуле:

2. Проверить критерии близости двух точек:

;

Если он выполняется, принять и остановиться.

Если не выполняется, то из 2-х точек b и d выбрать «лучшую» - в которой наименьшее значение функции, обозначить её как b, а 2 соседние с ней – a и c. Далее рассмотреть 4 ситуации аналогично ЗС-2.

3. Положить k=k+1 и вернуться на шаг 1.

Метод Давидона

Начальный этап

1. Выбрать ε, x⁰, p, α₁

2. Предполагается, что сработал метод Свенна и получен интервал [a, b].

Основной этап

1. Найти аппроксимирующий минимум, т.е. точку d по формулам:

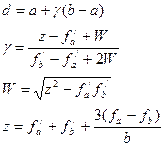
2. Проверить КОП: если y`<sub>r</sub>≤ ε, то остановиться, х=a+α<sub>r</sub>p. Иначе: сократить ТИЛ: если y`_r <0, то [r,b], если y`_r >0, то [a,r].

Положить k=k+1 и вернуться на шаг 1.

Методы многомерной минимизации

Здесь имеет смысл упомянуть о поиске минимума функции многих переменных по направлению, так как этом используется во многих методах описываемых далее. Поиск минимума по направлению производится с использованием одномерных методов, т.е. сначала многомерная функция сводится к одномерной функции зависящей от смещения по заданному направлению из заданной точки, а потом для неё вызывается один из методов одномерной минимизации:

x – вектор от которого зависит функция

x0 – стартовая точка

p – направление

L – смещение по направлению

Метод Коши

Метод Коши относится к группе методов градиентного спуска. Градиентные методы – это методы, где на каждом шаге выбирается антиградиентное направление спуска.

Начальный этап

Выбрать x1, e, k.

Основной этап

Шаг 1

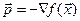
Шаг 2

(1) Найти L как результат минимизации функции по направлению p.

(2)

Шаг 3

(1) Вычислить новое значение градиента

(2) Проверить КОП: если 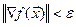, то , иначе на Шаг 1.

Поиск по сайту: