 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод Ньютона. Если f(x) является дважды дифференцируемой в Rn, то эффективность процесса поиска точки х* ее минимума можно повысить
Если f(x) является дважды дифференцируемой в Rn, то эффективность процесса поиска точки х* ее минимума можно повысить, используя информацию не только о градиенте этой функции, но и о ее матрице Гecce H(x). Алгоритмы такого поиска обычно относят к методу Ньютона. В простейшем варианте алгоритма на каждой k-й итерации целевая функция аппроксимируется в окрестности точки xk-1 (на первой итерации в окрестности начальной точки х0) квадратичной функцией 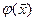 и затем определяется точка xk минимума функции
и затем определяется точка xk минимума функции 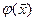 . На следующей, (k+ 1)-й итерации строится новая квадратичная аппроксимация уже в окрестности точки xk.
. На следующей, (k+ 1)-й итерации строится новая квадратичная аппроксимация уже в окрестности точки xk.
Начальный этап:
Выбрать x0, e, k =1.
Основной этап
Шаг 1
(1) Строится Ньютоновское направление:  - градиент в заданной точке, H – матрица Гессе
- градиент в заданной точке, H – матрица Гессе
(2) Найти  как результат решения системы уравнений
как результат решения системы уравнений 
(3) 
(4) 
Шаг 3
Проверить КОП: если  , то
, то  , иначе на Шаг 1.
, иначе на Шаг 1.
Метод Зангвилла
Начальный этап
Выбрать константу остановки e > 0 и начальную точку x1. Положить y1 = x1, k = j =1,  и перейти к основному этапу.
и перейти к основному этапу.
Основной этап
Шаг 1. Взять в качестве  оптимальное решение задачи минимизации
оптимальное решение задачи минимизации  при
при  и положить
и положить  . Если
. Если 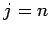 , то перейти к шагу 4; в противном случае перейти к шагу 2.
, то перейти к шагу 4; в противном случае перейти к шагу 2.
Шаг 2. Положить  и взять в качестве
и взять в качестве  оптимальное решение задачи минимизации
оптимальное решение задачи минимизации  при
при  . Положить
. Положить  ,
,  и перейти к шагу 3.
и перейти к шагу 3.
Шаг 3. Если  , то остановиться;
, то остановиться; 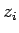 -- оптимальное решение. В противном случае взять в качестве
-- оптимальное решение. В противном случае взять в качестве  оптимальное решение задачи минимизации
оптимальное решение задачи минимизации 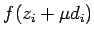 при
при  . Положить
. Положить 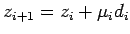 . Если
. Если  , то заменить
, то заменить  на
на  и повторить шаг 3. В противном случае положить
и повторить шаг 3. В противном случае положить 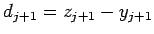 , заменить
, заменить 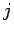 на
на  и перейти к шагу 1.
и перейти к шагу 1.
Шаг 4. Положить  ,
,  , заменить
, заменить  на
на 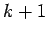 , положить
, положить 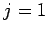 и перейти к шагу 1.
и перейти к шагу 1.
Метод Флетчера-Ривса
Метод сопряжённых направлений основан на свойствах векторов сопряженных относительно некоторой квадратной матрицы. Различие в способах построения системы сопряженных векторов, определяющих сопряжённые направления спуска, порождает несколько алгоритмов этого метода. В качестве матрицы сопряжений берётся матрица Гессе. Особенность алгоритмов метода сопряженных направлений состоит в том, что систему сопряженных векторов строят последовательно в процессе выполнения итераций, причем найденный на очередной, k-й итерации вектор pk определяет на этой итерации направление спуска. Для не квадратичных функций получаемые направления, в конце концов, перестают быть взаимносопряженными поэтому, как и в ДФП через n шагов вектор направления делают равным антиградиенту.
Начальный этап
Выбрать x1, e, k=1.
Основной этап
Шаг 1.
Построить вектор pk:

Шаг 2.
Найти новую точку  как результат одномерного поиска полученного направления
как результат одномерного поиска полученного направления  .
.
Шаг 3.
Проверить КОП:  .
.
Расчетное соотношение Флетчера-Ривса
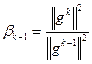
Метод Пауэлла
Метод достаточно прост в реализации и обладает квадратичной сходимостью вблизи минимума. Стратегия метода базируется на свойстве квадратичных функций параллельного подпространства: если x1 минимум квадратичной функции по вектору p, а x2 минимум этой же функции по вектору параллельному предыдущему, то  .
.
Первый вариант алгоритма метода Пауэлла
Начальный этап
(1) Выбрать x1, e, k=1.
(2) Положить 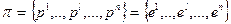
Основной этап:
Шаг 1.
(1) Выполнить n переходов по векторам базиса  :
: 
(2) Определить новое направление и спуститься вдоль него: 
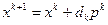
Шаг 2.
Проверить КОП: если  ,или k = n (для квадратичных функций) то прекратить поиск, иначе Шаг 3
,или k = n (для квадратичных функций) то прекратить поиск, иначе Шаг 3
Шаг 3.
Построить новую поисковую систему: из предыдущей системы удаляется первый вектор, а в конец добавляется вектор d.
Таким образом изменение системы поиска выглядит так:

Второй вариант алгоритма метода Пауэлла
Отличается от первого варианта тем, что изначально строится поисковая система где первый и последний вектор параллельны:

Изменение поисковой системы выглядит так:

Поиск по сайту: