 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм Фибоначчи-2
Начальный этап
(1) Задать константу e, начальный интервал [a1, b1], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1)/Ln.
(2) Выбрать одну пробную точку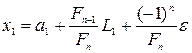 
. Положить
k = 1.
Основной этап
Шаг 1. Проверить критерий окончания поиска: если k=n, то остановиться и положить x*=x2.
Шаг 2. Сократить текущий интервал локализации рассмотрением 4-х ситуаций, аналогично методу золотого сечения-2.
Метод линейной интерполяции (метод секущих)
Метод секущих предлагает заменить вторую производную f ''(xk) в ньютоновской формуле её линейной аппроксимацией (f '(xk)-f '(xk-1))/(xk-xk-1).
Тем самым очередное приближение хk+1 к стационарной точке х* задаётся формулой вида
xk+1 = xk - f '(xk) * (xk - xk-1) / (f '(xk) - f '(xk-1)).
Легко видеть, что хk+1 - точка пересечения с осью абсцисс секущей прямой, проходящей через точки хk и хk-1.
В отличие от метода Ньютона метод секущих гарантирует сходимость точек {xk} к стационарной точке х*, однако, сходимость метода достигается ценой потери быстродейсвия. Как правило, метод дихотомии оказывается эффективнее метода секущих, хотя последний и получен из более быстродействующей схемы.
Начальный этап. Пусть методом Свенна получен интервал неопределённости [a1,b1], границы которого удовлетворяют неравенству f'(a1)f '(b1) < 0. Задать e - погрешность вычисления минимума и принять k= 1.
Основной этап
Шаг 1. Найти очередное приближение хk+1 к минимуму х* и проверить условие окончания поиска:
(1) xk+1 = bk - f '(bk)*(bk - ak)/(f '(bk) - f '(ak));
(2) если ½ f '(xk+1) ½ << e, то остановиться.
Шаг 2. Уменьшить интервал поиска минимума:
(1) если f '(xk+1) > 0, то ak+1 = ak, bk+1 = xk+1, в противном случае принять ak+1 = xk+1, bk+1 = bk;
(2) положить k = k + 1 и перейти на шаг 1.
Метод средней точки (метод Больцано)
Данный метод является вариантом метода деления интервала пополам. Последовательные сокращения интервала неопределенности производятся на основе оценки производной минимизируемой функции в центре текущего интервала.
Начальный этап. Для запуска метода необходимо:
(1) задать [a1,b1]- начальный интервал локализации минимума, на границах которого знаки производных различны, т.е. f'¢(a1)f'¢(b1)<0; e - малое положительное число;
(2) положить к=1 и перейти к основному этапу.
Основной этап
Шаг 1. Взять пробную точку хk в центре текущего интервала и проверить критерий окончания поиска: (1) xk = (ak + bk)/2; (2) если ½f'¢(xk)½ ≤ e и Lk= ½bk - ak½≤ e, то остановиться (хk = х* -аппроксимирующий минимум).
Шаг 2. Сократить текущий интервал:
(1) Если f ¢(xk) > 0, то положить ak+1 = ak и bk+1 =xk, в противном случае - ak+1 =xk, bk+1 =bk;
(2) заменить k на k+1 и вернуться на шаг 1.
Поиск по сайту: