Интерференционные минимумы

Для выяснения дальнейших деталей фраунгоферовой дифракционной картины воспользуемся векторной диаграммой, которая позволит легко найти и результирующую амплитуду А колебаний, приходящих в произвольную точку Р фокальной плоскости объектива.

Векторная диаграмма в данном случае представляет собой цепочку векторов-амплитуд когерентных колебаний, приходящих в точку Р от каждой из N щелей: А ₁, А ₂,..., А _N (рис.23,а). По модулю эти векторы одинаковы, и каждый следующий отстает от предыдущего (или опережает, это не существенно) по фазе на один и тот же угол g. Этот угол связан с оптической разностью хода D соответствующих лучей от соседних щелей соотношением:

, где d - период решетки (рис.22, б)

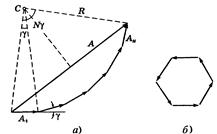
Рис.23

Теперь проследим, как будет вести себя эта цепочка векторов и ее замыкающая А при удалении точки Р от центра симметрии F (рис.22, а), т.е. с ростом угла дифракции . При этом будет увеличиваться разность фаз g между колебаниями от соседних щелей, и цепочка векторов будет постепенно закручиваться. Первый раз она замкнется и вектор А обратится в нуль, когда угол N g станет равным 2p - это непосредственно видно из рис.23, б.

При дальнейшем росте угла , цепочка будет периодически то распрямляться (главные максимумы, А = макс), то замыкаться (интерференционные минимумы, А = 0). Последнее будет происходить при значениях угла N g кратных 2p:

N g = 2p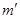

где 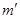принимает целочисленные значения, кроме 0, N, 2 N,..., при которых цепочка распрямляется, и мы получаем главные максимумы. Таким образом, условие для интерференционных минимумов можно записать в виде:

при целочисленных значениях 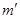(кроме 0, N, 2 N,...).

Оно же содержит и условие для главных максимумов (при 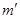= 0, N, 2 N,...). Между двумя соседними главными максимумами расположены N - 1 интерференционных минимумов. А между последними, в свою очередь, - добавочные максимумы, интенсивность которых при достаточно большом числе N штрихов решетки пренебрежимо мала (как будет видно из дальнейшего).

Последнее соотношение позволяет определить угловую ширину главных максимумов. В самом деле, при переходе от главного максимума к соседнему минимуму (рис.24) 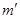меняется на единицу, например от N до N + 1. Тогда, при достаточно большом N, угловую полуширину 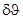главного максимума 1-го порядка можно найти, взяв дифференциал последнего уравнения с учетом того, что 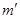при этом меняется на единицу (d 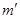= 1). Тогда 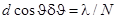, откуда

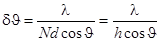
Рис.24

Обращает на себя внимание тот факт, что 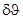зависит не от d и N в отдельности, а от их произведения, которое есть не что иное, как ширина решетки h = Nd. С ростом угла дифракции ширина главных максимумов увеличивается. Главные максимумы будут тем уже, чем больше ширина решетки h и меньше угол дифракции .

Оценим отношение угловой ширины главных максимумов к угловому расстоянию между ними. Это отношение характеризует «резкость» главных максимумов. Значение 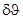соответствует изменению 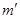на единицу, но таких значений 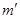между двумя соседними главными максимумами оказывается N. Поэтому приходим к выводу, что отношение равно N. Итак, резкость главных максимумов пропорциональна числу штрихов решетки.

Рассмотрим вначале качественно вопрос о интенсивности главных максимумов. Прослеживая с помощью рис.23 как будет вести себя векторная диаграмма по мере увеличения угла дифракции , мы оставили без внимания тот факт, что при этом каждый вектор цепочки по модулю будет изменяться, ибо он определяется дифракцией от каждой щели. Следовательно, кроме интерференционных минимумов, необходимо иметь в виду и дифракционные минимумы, определяемые условием

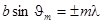, m = 1, 2,..., где b - ширина каждой щели.

При этом условии все векторы цепочки обращаются в нуль, значит и результирующая интенсивность в этих направлениях всегда должна быть равна нулю, даже в том случае, если этому направлению соответствует главный максимум m -ного порядка.

Интенсивность главных максимумов

Распределение интенсивности в дифракционной картине проще всего получить с помощью векторной диаграммы (рис.23,а). Из этой диаграммы видно, что результирующую амплитуду А при интерференции N волн можно записать так

,

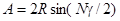где R - вспомогательный радиус дуги окружности, описанной вокруг данной цепочки векторов. Кроме того, амплитуда А ₁ колебаний от каждой щели, как видно из этого же рисунка, 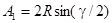. Исключив 2 R из последних двух формул, получаем:

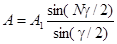
Учитывая, что

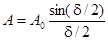, а также, что I ~ A ², получим окончательно:

,

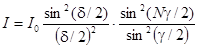где

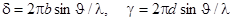
Полученный результат представлен на рис.25, как зависимость интенсивности дифракционной картины от 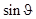. Как видим из рисунка, интерференция многих пучков привела к резкому перераспределению интенсивности света, обусловленной дифракцией от каждой щели. Первая дробь в последнем выражении представляет собой плавную функцию от 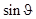(она показана пунктиром на рисунке и отражает дифракционное распределение интенсивности от каждой щели). Эта плавная функция модулирует многолучевую интерференционную картину от N щелей, которую описывает вторая дробь в формуле.

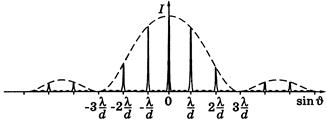
Рис.25

Практически наиболее важными являются главные максимумы, попадающие в центральный дифракционный максимум от каждой щели - они являются наиболее интенсивными.

Поиск по сайту: