 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракция Френеля от круглого отверстия
Зоны Френеля.
Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку Р, вообще говоря, весьма сложно. Но в простейших случаях, обладающих определенной симметрией, интегрирование, как показал Френель, может быть заменено простым алгебраическим или графическим сложением (последнее наиболее наглядно).
Суммирование амплитуд колебаний, приходящих от различных элементов волновой поверхности S, Френель предложил делать с помощью разбиения поверхности S на зоны, конфигурация которых зависит от симметрии рассматриваемой задачи.
Пользуясь методом Френеля, определим амплитуду световых колебаний в точке Р за круглым отверстием на его оси (рис.3). Волновая поверхность S, которой мы перекроем отверстие, симметрична относительно прямой Р 0 Р, поэтому ее наиболее целесообразно разбивать на кольцевые зоны, с центром на оси отверстия. Эти зоны выбираем так, чтобы расстояния от краев каждой зоны до точки Р отличались друг от друга на половину длины волны, l/2. Это и есть зоны Френеля в данном случае.
Рис.3
Найдем внешний радиус m -й зоны Френеля, rm. С этой целью воспользуемся рис.4.
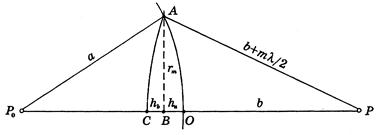
Рис.4
Видно, что отрезок СО равен
ha + hb = m l/2
Далее
; ha = 
; hb = 
Таким образом,
Отсюда получаем внешний радиус m -й зоны Френеля:
Если на отверстие падает нормально плоская волна (а ® ¥)
Площади зон (при достаточно малых m)
т.е. практически одинаковы. Но амплитуды колебаний, приходящих в точку Р от этих зон, монотонно и слабо убывают из-за увеличения расстояния r до точки Р от каждой следующей зоны и роста угла 
между нормалью к элементам зоны и направлением на точку Р.
Фазы колебаний, возбуждаемых в точке Р соседними зонами, отличаются на p, поэтому векторы-амплитуды нечетных зон противоположны по направлению векторам амплитудам от четных зон. И результирующая амплитуда, а значит и интенсивность, зависит от того, четное или нечетное число m зон Френеля умещается в отверстии - для точки наблюдения Р. Если число зон нечетное, то в точке Р наблюдается максимум, если же число зон четное, то - минимум.
Число зон m в отверстии мы можем изменять. Например, для увеличения числа зон надо или расширить отверстие, или приблизить экран к нему, или и то и другое вместе. Это непосредственно вытекает из полученной формулы для радиуса зон, если под rm понимать радиус отверстия.
Поиск по сайту: