Дифракция Фраунгофера от круглого отверстия

Дифракция Фраунгофера от круглого отверстия представляет большой практический интерес, поскольку в оптических приборах оправы линз и объективов, а также диафрагмы имеют обычно круглую форму.

Дифракционную картину Фраунгофера от круглого отверстия в преграде N можно наблюдать на экране Э в фокальной плоскости линзы L, направив на отверстие нормально плоскую световую волну (рис.16, а). Эта картина имеет вид центрального светлого пятна, окруженного чередующимися темными и светлыми кольцами. Соответствующий расчет (приводить его не будем) дает, что минимум первого темного кольца отстает от центра дифракционной картины на угловое расстояние

- это при условии, что диаметр отверстия D >>l, что чаще всего и бывает.

На рис.16, б показана зависимость интенсивности света I от углового радиуса (угла дифракции), здесь О - центр дифракционной картины. Из формулы следует, что размер дифракционной картины тем меньше, чем больше диаметр отверстия D. Подавляющая часть светового потока (84%), проходящего через отверстие, попадает в область центрального светлого пятна. Поэтому в первом приближении дифракционную картину можно считать состоящей из одного лишь светлого пятна с угловым радиусом , определяемым ранее приведенной формулой. И центральное светлое пятно можно рассматривать как изображение удаленного точечного источника, уширенное дифракцией от краев круглого отверстия диаметра D.

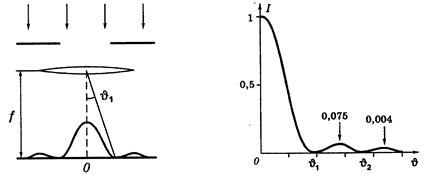
Рис.16

Следует обратить внимание на то, что в центре фраунгоферовой дифракционной картины от круглого отверстия всегда образуется максимум (в отличие от френелевой дифракции, когда в центре может образоваться как максимум, так и минимум).

Дифракционная расходимость пучка

Полученные результаты можно использовать для оценки дифракционной расходимости пучков света, диаметр которых ограничен, например, в результате прохождения плоской световой волны через отверстие (или диафрагму). Учитывая, что основная часть светового потока, проходящего через отверстие, приходится на центральный дифракционный максимум, его ширину можно принять в качестве оценки угловой расходимости dq пучка с первоначальным диаметром поперечного сечения D:

dq ~ l/ D

Таким образом, принципиально (из-за дифракции) невозможно создать совершено параллельный ограниченный в сечении пучок света. Этим уширением можно пренебречь лишь в тех случаях, когда оно мало по сравнению с исходной шириной пучка.

Разрешающая способность объектива

Вследствие волновой природы света изображение точки, даваемое линзой, имеет вид дифракционного кружка - результат дифракции света на оправе линзы. Так как свыше 80% проходящего через линзу светового потока приходится на центральное светлое пятно, то в дальнейшем на окружающие его кольца можно не обращать внимания.

Теперь рассмотрим два одинаковых некогерентных точечных источника. Если расстояние между центрами их изображений мало по сравнению с размерами центральных светлых пятен, то результирующая картина практически не отличается от изображения одного точечного источника. И тогда считают, что объектив не разрешает рассматриваемые точки.

Начиная с некоторого расстояния между центрами обоих светлых кружков, между ними появляется темный провал, и это будет восприниматься как раздельное изображение двух точек. Объектив, как говорят, будет разрешать эти точки.

Условный критерий разрешающей способности был предложен Рэлеем. Согласно критерию Рэлея, два точечных некогерентных источника считаются разрешенными, если центр дифракционного пятна от одного из них совпадает с ближайшим к центру минимумом дифракционной картины от другого. Это соответствует минимальному угловому расстоянию между источниками, определяемому формулой

Результирующая картина показана на рис.17, где провал составляет около 25% от максимума интенсивности.

Рис.17

Величину, обратную предельному углу, называют разрешающей способностью (или разрешающей силой):

Видим, что разрешающая способность объектива пропорциональна его диаметру.

Глаз при рассматривании удаленных предметов действует в принципе так же, как объектив. Роль величины D играет диаметр d зрачка глаза. Полагая d» 4 мм, l = 0,55 мкм, находим, что разрешаемое угловое расстояние глазом

угл. сек.

Этот результат удивительно хорошо согласуется с физиологической оценкой разрешающей способности глаза, связанной со структурой его сетчатки (как будто при конструировании человеческого организма учитывались принципиальные ограничения разрешающей способности, обусловленные волновой природой света).

Поиск по сайту: