Дифракция Фраунгофера от щели. Рассмотрим случай, когда на щель ширины b падает нормально плоская световая волна (рис.18)

Рассмотрим случай, когда на щель ширины b падает нормально плоская световая волна (рис.18). Разобьем мысленно эту щель - она же открытая часть волновой поверхности - на очень узкие одинаковые по ширине зоны-полоски, параллельные прямоугольным краям щели. Суммирование вторичных волн проведем с помощью векторной диаграммы.

Рис.18

Колебание, возбуждаемое в точке наблюдения каждой зоной-полоской, имеет одинаковую амплитуду dА и отстает по фазе от предыдущего колебания на одну и ту же величину, зависящую от угла , определяющего направление на точку наблюдения Р (рис.18). Отсюда следует, что при графическом изображении мы получим цепочку векторов d А _i, одинаковых по модулю и повернутых относительно друг друга на один и тот же угол. Результирующая амплитуда изобразится вектором А - хордой дуги окружности с центром в точке С (рис.19).

Рис.19

Распределение интенсивности

Найдем интенсивность I света на экране в зависимости от угла дифракции . Это легко сделать с помощью рис.19. Обозначив радиус цепочки-дуги через R, запишем:

А = 2 R sin (d/2), A ₀ = R d

Остается исключить R из этих двух равенств, и мы получим:

А так как I ~ A ², то искомая зависимость будет иметь вид:

где a = d/2 = pD/l = pb sin /l

График зависимости I от sin показан на рис.20. Интенсивность второго максимума составляет около 4% от интенсивности центрального, поэтому можно считать, что практически весь световой поток. проходящий через щель, сосредоточен в первом (центральном) максимуме, угловая ширина которого равна l/ b. Этот результат согласуется со случаем дифракции Фраунгофера от отверстия, определяющей дифракционную расходимость «параллельных» световых пучков ограниченного сечения.

Рис.20

Если плоская световая волна падает на щель наклонно под углом ₀ к нормали, то разность хода между колебаниями, распространяющимися от краев щели под углом к нормали, будет равна . Это при условии, что оба угла, и ₀, отсчитываются от нормали в одну сторону - по или против часовой стрелки.

Условие дифракционных минимумов в данном случае принимает вид

Центральный максимум (m = 0) будет расположен под углом _m = ₀, т.е. в направлении падающей волны, и дифракционная картина будет несимметрична относительно центральной светлой полосы.

Рассмотрим, как можно найти интенсивность в максимумах дифракционной картины с помощью векторной диаграммы.

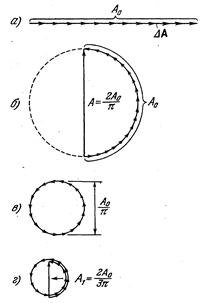
Рис.21

При = 0 разность фаз d равна нулю и векторная диаграмма имеет вид, показанный на рис.21, а. Амплитуда результирующего колебания А ₀ равна сумме амплитуд складываемых колебаний. Если D = b sin = l/2, колебания от краев щели находятся в противофазе. Соответственно векторы D А располагаются вдоль полуокружности длиной А ₀ (рис.21, б). Следовательно, результирующая амплитуда равна 2 А ₀/p. В случае, когда D = b sin = l, колебания от краев щели находятся в противофазе. Соответственно векторы D А располагаются вдоль окружности длиной А ₀. результирующая амплитуда равна нулю - получается первый минимум (рис.21, в). Первый максимум получается при D = b sin = 3l/2. В этом случае колебания от краев щели отличаются по фазе на 3p. Строя последовательно векторы D А, мы обойдем полтора раза окружность диаметра А ₁ = (2/3p) А ₀ (рис.21, г). Диаметр этой окружности и есть амплитуда первого максимума. Таким образом, интенсивность первого максимума равна I ₁ = (2/3p)² I ₀» 0,045 I ₀. Аналогично можно найти и относительную интенсивность остальных максимумов. В итоге получится следующее соотношение:

Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы; в нем сосредоточена основная доля светового потока, проходящего через щель.

Поиск по сайту: