Дифракция Френеля от полуплоскости и щели

Перейдем к случаю, когда волновая поверхность плоская и характер препятствия (полуплоскость, щель) предписывает разбивать открытую часть волновой поверхности на зоны в виде прямолинейных полосок.

Дифракция от прямолинейного края полуплоскости

Пусть на экран Э падает нормально плоская монохроматическая волна длины l. Расположим перед экраном на расстоянии l от него непрозрачную полуплоскость N с прямолинейным краем (рис.9). Если бы свет распространялся прямолинейно, то на экране Э мы наблюдали бы резкую тень от края этой полуплоскости (точка Р ₀ на рис.9). В действительности же из-за волнового характера света на экране Э образуется сложная дифракционная картина. Расчеты этой картины были проведены аналитически Френелем, получены результаты в виде так называемых интегралов Френеля.

Рис.9

Ограничимся интерпретацией этого расчета и полученного результата с помощью векторной диаграммы.

Из соображений симметрии ясно, что дифракционная картина на экране Э будет зависеть только от расстояния до границы геометрической тени - точки Р ₀ на рис.9, т.е. светлые и темные полосы должны быть параллельны прямолинейному краю К непрозрачной полуплоскости N. Говоря далее об амплитуде колебаний в точке Р на экране, мы будем иметь в виду, что это относится ко всем точкам прямой, проходящей через точку Р и параллельной краю полуплоскости.

В соответствии с симметрией данной задачи разобьем мысленно открытую часть волновой поверхности S на весьма узкие одинаковой ширины прямолинейные полоски (зоны), параллельные краю полуплоскости.

Амплитуду колебаний, приходящих в точку Р ₀ от первой зоны полоски изобразим вектором d A ₁ (рис.10). Амплитуду колебаний от следующей полоски - вектором d A ₂, повернутым на очень небольшой угол против часовой стрелки, так как эти колебания проходят до точки Р ₀ несколько большее расстояние и, значит, отстают по фазе.

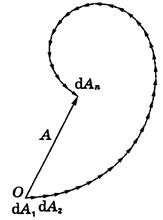
Рис.10

В дальнейшем угол между соседними векторами-амплитудами становится все больше, поскольку запаздывание по фазе колебаний, приходящих в точку Р ₀ от последующих зон-полосок растет все больше. Модули же векторов d A _i будут уменьшаться (из-за увеличения расстояния до точки Р ₀ и угла между нормалью к полоске и направлением на точку Р ₀).

Результирующая амплитуда колебаний в точке Р ₀ от достаточно широкой полосы волновой поверхности S изобразится суммой (цепочкой) векторов d A _i от всех укладывающихся на этой полосе элементарных зон-полосок. Это вектор А на рис.10.

Поиск по сайту: