 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 2. Ограниченная последовательность – если существует некое число M, что для любого xn по модулю меньше M
Ограниченная последовательность – если существует некое число M, что для любого xn по модулю меньше M.
│xn│< M
Ограниченная сверху последовательность — это последовательность элементов множества 
, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
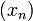ограниченная сверху 
Ограниченная снизу последовательность — это последовательность элементов множества , для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
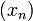ограниченная снизу 
Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.
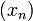ограниченная 
Неограниченная последовательность — это последовательность, которая не является ограниченной.
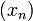неограниченная 
Поиск по сайту: