Вопрос 5. Теорема: Если { хn} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

Теорема: Если { х_n} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

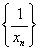
бесконечно малая, и, обратно, если {α_n} — бесконечно малая последовательность и все её члены отличны от нуля {α_n} ≠ 0, то последовательность { 1 / α_n } – бесконечно большая.
Доказательство. Пусть { х_n} — бесконечно большая последовательность. Возьмем любое как угодно малое положительное число ε > 0 и положим

Согласно определению для этого существует такой номер N, что при n > N будет | x_n | > A. Отсюда получаем, что

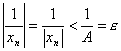
для всех n > N. А это значит, что последовательность

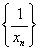
бесконечно малая.

Поиск по сайту: