Основное уравнение нерелятивистской квантовой механики___________________

Статистическое толкование волн де Бройля 6.22 и соотношение неопределенностей Гейзенберга 6.18 привели к выводу, что уравнением движе­ния в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытека­ли наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции ЧХх, у, г, I), так как именно она, или, точнее, величина I^х?!², определяет вероятность пребывания частицы в момент времени I в объеме (IV, т. е. в области с координатами х и х + Ах, у иг/ + Ау, гшг + Аг. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему элек­тромагнитные волны.

Временное уравнение Шредингера__________________________________________________

Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых с его помощью результатов.

Условия, накладываемые на волновую функцию______________________________________

♦ Волновая функция должна: быть конечной, однозначной и непрерывной.

♦ Производные —должны быть непрерывны.

♦ Функция |Ψ|² должна быть интегрируема (это условие сводится к усло­вию нормировки вероятностей 6.22).

♦ Уравнение Шредингера справедливо для нерелятивистских частиц (скорости υ «с). [ , т — масса частицы, Δ — оператор Лапласа 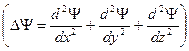, i- мнимая единица, U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y,z,t) — искомая волновая функция частицы]

Поиск по сайту: