АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Следствия уравнения Шредингера для квантового осциллятора________________

Читайте также:
  1. Flх.1 Употребление с вредными последствиями
  2. I I. Тригонометрические уравнения.
  3. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  4. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  5. V2: Применения уравнения Шредингера
  6. V2: Уравнение Шредингера
  7. V2: Уравнения Максвелла
  8. V3: Перестройка социально-политической жизни государства и ее последствия.
  9. VI Дифференциальные уравнения
  10. Автокорреляция случайного возмущения. Причины. Последствия.
  11. Алгебраические уравнения
  12. Алгебраические уравнения

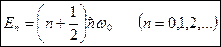Собственные значения энергии __________________________________________________

 

Уравнение Шредингера имеет однозначные, конечные и непрерывные решения только при таких Еп, т. е. энергия квантового осциллятора может иметь лишь дискретные решения (квантуется).

[ω0 — собственная частота колебаний осциллятора; — постоянная Планка; Еп — собственные значения энергии; Е0 — энергия нулевых колебаний]

Расстояние между соседними уровнями ___________________________________________

Уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (на рисунке 6.59 они изображены горизонтальными прямыми)


Энергия нулевых колебаний ___________________________________________________

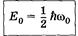Ее существование типично для квантовых систем; следствие соотношения неопределенностей: частица не может находиться на дне потенциальной ямы независимо от ее формы. Если бы это было возможно, то импульс, а также его неопределенность, обращались бы в нуль. Тогда неопределенность координаты , что противоречит пребыванию час­тицы в потенциальной яме.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)