АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свойства собственных функций______________________________________________

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. II. Свойства векторного произведения
  3. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  4. LU – алгоритм нахождения собственных значений для несимметричных задач
  5. QR- алгоритм нахождения собственных значений
  6. V2: Электрические и магнитные свойства вещества
  7. Абсолютная и условная сходимость несобственных интегралов.
  8. Аксиомы ординалистского подхода. Функция полезности и кривые безразличия потребителя. Свойства кривых безразличия. Предельная норма замещения
  9. Акустические свойства голоса
  10. Акустические свойства горной породы.
  11. Акустические свойства строительных материалов
  12. Алгебраические свойства векторного произведения

Уравнение для собственных функций и собственных значений оператора _____________

В уравнении — оператор, отвечающий данной физической величине; если оператор воспроизводит функцию Ψ с точностью до множителя L, то Ψ — собственная функция оператора , а множитель L— собст­венное значение оператора .

♦ Функция Ψ удовлетворяет стандартным условиям (определена по всей об­ласти независимых переменных, непрерывна, однозначна и конечна) и условию квадратичной интегрируемости (интеграл сходится).

Взаимно ортогональные собственные функции _____________________________________

Собственные функции и 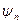линейного эрми това оператора , отвечающие различным соб­ственным значениям и , взаимно ортогональны, если они отвечают записанному условию.

Ортогональные и нормированные системы функций _______________________________

Предыдущее равенство объединено с условием нормировки вероятностей 6.22.

В квантовой механике используются эрмитовы операторы, так как соб­ственные значения эрмитовых операторов — действительные числа.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)