 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определить накопленную сумму к концу срока ренты
Схематично условие задачи показано на рисунке.
100 тыс. руб. 100 тыс. руб. 100 тыс. руб.
 |  |  |

 ·-------- S-?
·-------- S-?
01.01.1998 01.01.1999 01.01.2000 01.01.2001
Введем обозначения:
R — величина члена ренты;
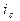 — cложная процентная ставка;
— cложная процентная ставка;
n — срок ренты в годах.
Все члены ренты, кроме последнего, приносят проценты: на первый проценты начисляются (n-1) год, на второй — (n-2) года и т.д. На последний член проценты не начисляются.
Наращенные суммы к концу срока ренты составят:
На 1-й член 
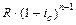
На 2-й член 
На (n-1)-й член 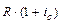
На n-й член — R
Накопленная сумма к концу срока ренты составит сумму членов этого ряда, который, если его переписать в обратном порядке, является возрастающей геометрической прогрессией, где R — 1-й член прогрессии, а величина (1 + 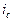 ) — знаменатель прогрессии. Сумму членов ряда, то есть наращенную сумму ренты, можно определить по формуле:
) — знаменатель прогрессии. Сумму членов ряда, то есть наращенную сумму ренты, можно определить по формуле:
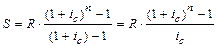 (3.1)
(3.1)
Величина  называется коэффициентом наращения ренты, который обозначим как
называется коэффициентом наращения ренты, который обозначим как 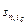 , где подстрочные символы указывают на срок ренты и применяемую процентную ставку. Тогда формула (3.1) примет вид:
, где подстрочные символы указывают на срок ренты и применяемую процентную ставку. Тогда формула (3.1) примет вид:
 . (3.2)
. (3.2)
Значение коэффициента 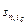 , а также значения ряда других финансовых коэффициентов, могут быть найдены из таблиц, имеющихся в любом учебном издании по финансовым вычислениям, в том числе и в данных рекомендациях. Кроме того, финансовые коэффициенты могут быть вычислены на компьютере с помощью финансовых функций, входящих в процессор Еxcel. Имеются также финансовые калькуляторы, предназначенные для проведения подобных расчетов.
, а также значения ряда других финансовых коэффициентов, могут быть найдены из таблиц, имеющихся в любом учебном издании по финансовым вычислениям, в том числе и в данных рекомендациях. Кроме того, финансовые коэффициенты могут быть вычислены на компьютере с помощью финансовых функций, входящих в процессор Еxcel. Имеются также финансовые калькуляторы, предназначенные для проведения подобных расчетов.
По данным примера 1 рассчитаем наращенную сумму ренты:
 тыс. руб.
тыс. руб.
Предположим, что в примере 1 взносы будут вноситься не в конце,
а начале каждого года. В этом случае имеем ренту пренумерандо. Каждый член такой ренты «работает» на один период больше, чем в ренте постнумерандо. Отсюда наращенная сумма ренты пренумерандо, обозначим ее как 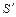 , больше в (1+
, больше в (1+  ) раз наращенной суммы аналогичной ренты постнумерандо.
) раз наращенной суммы аналогичной ренты постнумерандо.
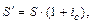 (3.3)
(3.3)
где S — наращенная сумма финансовой ренты постнумерандо.
В примере 1 для взносов в начале года наращенная сумма к концу срока ренты составит:
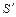 = 337,44 × (1+0,12) = 377,9328 тыс. руб.
= 337,44 × (1+0,12) = 377,9328 тыс. руб.
Нами был рассмотрен метод расчета наращенной суммы, когда рентный платеж производится один раз в году и начисление процентов также раз в году. Вместе с тем, в контрактах могут предусматриваться и другие условия поступления рентных платежей и порядок начисления процентов на них.
Рассмотрим ряд вариантов.
1) Рентные платежи вносятся один раз в году, а проценты на них начисляются m раз в году. В этом случае начисление процентов каждый раз будет производиться по ставке j/m, где j — номинальная (годовая) ставка сложных процентов.
Величина наращенной суммы ренты постнумерандо будет определяться по формуле:
 . (3.4)
. (3.4)
Величина наращенной суммы ренты пренумерандо в этом случае будет определяться по формуле:
 . (3.5)
. (3.5)
Пример 2. Несколько изменим условия примера 1. Пусть теперь проценты начисляются два раза в год. Рента постнумерандо.
| Имеем: j = 0,12 m = 2 R = 100 тыс. руб. n = 3 | Решение: Так как рента годовая, постнумерандо, проценты начисляются два раза в год, то наращенная сумма определяется по формуле (1.4.): |
| S=? |  тыс. руб. тыс. руб.
|
2) Рентные платежи вносятся несколько раз в году равными суммами (р-срочная рента), а начисление процентов производится один раз в конце года.
Если годовая сумма платежей равна R, то каждый раз выплачивается  (p — количество выплат в году). Общее число членов ренты равно n × p. Ряд членов ренты постнумерандо с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен
(p — количество выплат в году). Общее число членов ренты равно n × p. Ряд членов ренты постнумерандо с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен 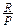 , знаменатель —
, знаменатель — 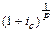 .
.
Сумма членов этой прогрессии:
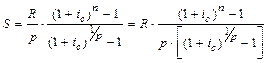 . (3.6)
. (3.6)
Наращенная сумма для ренты пренумерандо в данной ситуации будет определяться по формуле
 . (3.7)
. (3.7)
Пример 3. Еще раз изменим условия примера 1, допустив, что ежегодный взнос разбивается на 4 равные части, которые будут вноситься в банк в начале каждого квартала:  тыс. руб.
тыс. руб.
Определить накопленную сумму к концу срока ренты.
| Имеем: R = 100 тыс. руб. р = 4 ic = 0,12 n = 3 | Решение: Так как рента срочная (поквартальная), пренумерандо, проценты начисляются на платежи один раз в год, то наращенная сумма определяется по формуле (3.7.): |
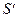 -? -?
| 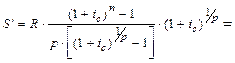
 = 100362,392 тыс. руб.
= 100362,392 тыс. руб.
|
3) Рентные платежи вносятся несколько раз в году (р-срочная рента), число периодов начисления процентов в течение года равно числу рентных платежей (m = p).
В этом случае наращенная величина финансовой ренты постнумерандо:
 . (3.8)
. (3.8)
Наращенная сумма ренты пренумерандо:
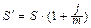 . (3.9)
. (3.9)
4) Рентные платежи вносятся р в году, начисление процентов – m раз в году; причем р 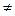 m.
m.
Наращенная сумма для ренты постнумерандо:
 . (3.10)
. (3.10)
Наращенная сумма для ренты пренумерандо:
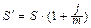
 (3.11)
(3.11)
Пример 4. В условиях примера 3, допустим, что проценты на взносы будут начисляться в конце каждого полугодия. Определить наращенную сумму для ренты постнумерандо.
| Имеем: R = 100 тыс. руб. р = 4 m = 2 j = 0,12 n = 3 | Решение:
Так как рента срочная (поквартальная), постнумерандо, проценты начисляются два раз в год, то наращенная сумма определяется по формуле (3.10): 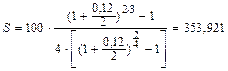 тыс. руб. тыс. руб.
|
| S =? |
Рассмотрены четыре примера определения наращенной суммы постоянной финансовой ренты. Сопоставив полученные результаты между собой, можно заметить, что величины наращенных сумм изменялись в зависимости от изменения условий ренты.
Зная, как влияют эти причины на данную характеристику финансовой ренты, целесообразно их использовать для получения наиболее выгодных условий при заключении контрактов.
Поиск по сайту: