 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Элементы теории игр
План.
- Основные понятия. Платежная матрица игры.
- Решение игр в смешанных стратегиях. Элементарные приемы решения игр 2x2.
- Сведение решения игры к задаче линейного программирования.
1.
Финансово-экономические операции в условиях рыночных отношений часто характеризуются наличием противоположных интересов различных оперирующих сторон, которые пытаются достичь своих целей часто в ущерб друг другу.
В этой связи при разработке управленческого решения в условиях конфликта особое место занимают выбор и сравнительный анализ возможных (допустимых) способов (стратегий) действий.
Конфликт может проявляться не только в результате сознательных действий различных участников, но и как результат действия тех или иных «стихийных сил» (случай так называемых «игр с природой»). Множество подобных примеров можно встретить в биологии, социологии, психологии, политологии, военном деле и т.д.
Раздел теории операций, связанный с математическим моделированием конфликта и поиском оптимальных решений в его условиях, называют теорией игр. В этой связи математическую модель конфликта часто называют игрой.
Стороны, участвующие в конфликте называются игроками, а исход конфликта – выигрышем. Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая: 1) варианты действий игроков; 2) объем информации каждого игрока о поведении партнеров; 3) выигрыш к которому приводит каждая совокупность действий.
Выбор и осуществление одного из предусмотренными правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий (например, в шахматной игре). Случайный ход – это случайно выбранное действие (например, выбор карты из перетасованной колоды). Будем рассматривать только личные ходы.
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации. Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации. Однако в принципе, возможно, что все решения приняты игроком заранее. Это означает, что игрок выбрал определенную стратегию, которая может быть задана в виде списка правил и программы. Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной – в противном случае.
Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Будем рассматривать только парные игры. В них участвуют два игрока А и В интересы которых противоположны, а под игрой будем понимать ряд действий со стороны А и В.
Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого, т.е. для полного задания игры достаточно указать величину одного из них.
Для того чтобы решить игру, или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными.
Целью теории игр является оптимальной стратегии для каждого игрока. При выборе оптимальной стратегии естественно предполагать, что оба игрока ведут себя разумно с точки зрения своих интересов.
Замечание. Важнейшее ограничение теории игр – единственность выигрыша как показателя эффективности, в то время как в большинстве реальных экономических задач имеется более одного показателя эффективности. Кроме того, в экономике, как правило, возникают задачи, в которых интересы партнеров не обязательно антагонистические.
Платежная матрица. Нижняя и верхняя цена игры.
Рассмотрим парную конечную игру. Пусть игрок А располагает m личными стратегиями, которые обозначим А1, А2, …Аm. Пусть у игрока В имеется n личных стратегий, обозначим их В1, В2, …Вn. Говорят, что игра имеет размерность m x n. В результате выбора игроками любой пары стратегий Ai и Bj однозначно определяется исход игры, т.е., выигрыш аij игрока А (положительный или отрицательный) и проигрыш (-aij) игрока В. Предположим, что значения aij известны для любой пары стратегий (Ai, Bj). Матрица P = (aij), элементами которой являются выигрыши, соответствующие стратегиям Ai и Bj, называется платежной матрицей или матрицей игры. Общий вид такой матрицы представлен в виде таблицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрок В.
| В1 | В2 | … | Вn | |
| А1 | a11 | a12 | … | a1n |
| А2 | a21 | a22 | … | a2n |
| … | … | … | … | … |
| Аm | am1 | am2 | … | amn |
Рассмотрим игру m x n с матрицей P = (aij) и определим наилучшую среди стратегий А1, А2,…, Аm. Выбирая стратегию Аi, игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий Bj, для которой выигрыш для игрока А минимален (игрок В стремится «навредить» игроку А).
Обозначим через αi наименьший выигрыш игрока А при выборе им стратегии Аi для всех возможных стратегий игрока В (наименьшее число в I- ой строке платежной матрицы), т.е.
 (1)
(1)
Среди всех чисел αi выберем наибольшее: α = max αi. Назовем α нижней ценой игры, или максиминным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно,
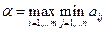 (2)
(2)
Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А. Выбирая стратегию Вj, он учитывает при этом максимально возможный при этом выигрыш для А. Обозначим
 (3)
(3)
Среди всех βj выберем наименьшее β = min βj и назовем β верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Следовательно,
 (4)
(4)
Стратегия, соответствующая минимаксу, называется минимаксной стратегией.
Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакс а. Этот принцип исходит из того, что каждый игрок стремится достичь цели, противоположной цели противника.
Теорема. Нижняя цена конечной антагонистической игры не превосходит верхней цены игры.
Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры α = β = ν называется чистой ценой игры или ценой игры.
Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность – оптимальным решением, или решением игры.
Пара чистых стратегий Аi и Вj дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент aij является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такой элемент, если он существует, называется седловой точкой матрицы платежей, а игра называется игрой с седловой точкой. Матричная антагонистическая игра, для которой α = β называется вполне определенной, или игрой, имеющей решение в чистых стратегиях.
Пример 1. Найти оптимальные стратегии игроков и цену игры, заданной платежной матрицей

Имеет ли игра седловую точку?
Поиск по сайту: