Решение. Найдем нижнюю цену игры:

Найдем нижнюю цену игры:

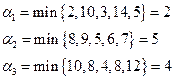
Нижняя цена игры α = .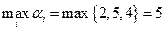

Найдем верхнюю цену игры:

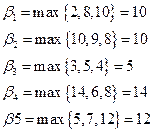
Верхняя цена игры β = .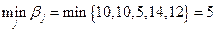

Как видим α = β = 5. Таким образом, цена игры ν = 5. Имеем седловую точку (2, 3).

Придерживаясь чистой второй стратегии, первый игрок обеспечивает себе выигрыш не меньший 5, а второй игрок применяя чистую третью стратегию, проигрывает не более 5. Обе стратегии являются оптимальными для первого и второго игроков.

Пример 2. Игра заключается в том, что игрок А записывает числа 1 (стратегия А1) или 2 (стратегия А2) или 3 (А3). Игрок В, в свою очередь, может записать числа 1 (В1), 2 (В2), 3 (В3) или 4 (В4). Если оба числа окажутся равной четности, то А выигрывает сумму этих чисел, если разной четности, то В выигрывает сумму этих чисел. Составить платежную матрицу игры, определить верхнюю и нижнюю цену игры и минимаксные стратегии.

Решение. Игрок А может выбрать одну из своих стратегий А1, А2 или А3. Игрок В может применить одну из своих стратегий В1, В2, В3 или В4. Если игрок А применяет стратегию А1, то есть записывает 1, а игрок В применяет стратегию В1 (так же записывает 1), т.е., осуществляется пара стратегий (А1, В1). Каждый из игроков записал нечетное число, следовательно, согласно условию, сумму этих чисел, т.е. 2 выигрывает игрок А. В таблице на пересечении А1, В1 записываем 2.

Если игрок А применяет туже стратегию А1, а игрок В применяет стратегию В2, т.е., записывает 2, то так как 1 – число нечетное, а 2 – число четное, то согласно условию сумму этих чисел выигрывает игрок В. Таким образом, на пересечении А1 и В2 необходимо записать -3 и т.д.

В результате получаем следующую таблицу или платежную матрицу игры.

Bj Ai	В1	В2	В3	В4	αi
A1		-3		-5	-5
A2	-3		-5		-5
A3		-5		-7	-7
βj					-5

Нижняя цена игры α = 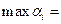-5.

Верхняя цена игры β = 4.

Таким образом, для игрока А максиминными стратегиями являются А1 и А2, при которых ему обеспечен выигрыш не менее –5 (т.е., проигрыш не более 5).

Для игрока В минимаксными стратегиями являются В1 и В2, обеспечивающие проигрыш не более 4.

Игра не имеет седловой точки, так как α < β.

2.

Решение игр в смешанных стратегиях.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий Аi с вероятностями р_i, причем сумма вероятностей 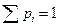. Смешанные стратегии игрока А записываются в виде матрицы 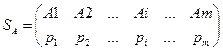или в виде строки . Аналогично определяются смешанные стратегии игрока В: , где .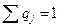

Чистые стратегии можно считать частным случаем смешанных и задавать единичным вектором-строкой, в котором 1 соответствует чистой стратегии. На основании минимакса определяется оптимальное решение игры. Цена игры удовлетворяет следующему неравенству:

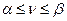(5),

где α и β – нижняя и верхняя цены игры.

Справедлива следующая основная теорема теории игр – теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры ν, если второй игрок не выходит за пределы своих активных стратегий.

Теорема о минимаксе. Всякая матричная не полностью определенная игра с нулевой суммой имеет решение для любой матрицы выигрышей и, кроме того, , где 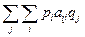– математическое ожидание (среднее ожидаемое значение) выигрыша игрока А.

Рассмотрим решение игры размера 2 х 2.

Если такая игра имеет седловую точку, то оптимальное решение это пара чистых стратегий, соответствующих этой точке.

Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S_A = (р1, р2) и S_B = (q1, q2). Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии S_A, то его средний выигрыш будет равен цене игры ν, какой бы активной стратегией не пользовался игрок В. Для игры 2 х 2 любая чистая стратегия является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) – случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен ν и для 1-ой и для 2-й стратегий противника.

Пусть игра задана платежной матрицей

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию S_A = (р1, р2), а игрок В – чистую стратегию В1 (первый столбец матрицы Р) равен цене игры ν:

.

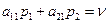Тот же средний выигрыш получает игрок А, если 2-ой игрок применяет стратегию В2, т.е.

.

Учитывая, что 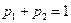, получаем систему уравнений для определения оптимальной стратегии S_A и цены игры ν:

Применяя теорему об активных стратегиях при отыскании S_В – оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А средний проигрыш игрока В равен цене игры ν, т.е.

Пример 3. Игрок А может спрятаться в одном из двух убежищ. Игрок В ищет игрока А, и если найдет, то получает штраф 1 у.е. от игрока А, в противном случае платит игроку А 1 у.е. Необходимо построить платежную матрицу игры, найти оптимальные стратегии и цену игры.

Решение. Составим платежную матрицу игры. Игрок А может спрятаться в убежище I – стратегия А1, либо в убежище II– стратегия А2.

Игрок В может искать игрока А в убежище I – стратегия В1, либо в убежище II– стратегия В2. Если игрок А находится в убежище I и там его обнаруживает игрок В, т.е., осуществляется пара стратегий (А1, В1), то игрок А платит штраф, т.е. а₁₁ = -1. Аналогично получаем а₂₂ = -1. Очевидно, что стратегии (А1, В2) и (А2, В1) дают игроку А выигрыш 1. Таким образом, получаем платежную матриц

Седловая точка отсутствует так как α = -1, а β = 1. Будем искать решение в смешанных стратегиях; для игрока А средний выигрыш равен цене игры ν (при В1 и В2); для игрока В средний проигрыш равен цене игры ν (при А1 и А2). Системы уравнений имеют вид:

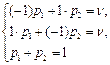
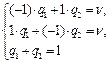
Решая эти системы, получаем р₁ = р₂ = q₁ = q₂ = ½. ν = 0.

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью ½, при этом средний выигрыш равен 0.

Геометрический метод решения игры 2 х 2.

Основные этапы решения игр 2 х 2 геометрическим методом.

1. Строят прямые, соответствующие стратегиям второго (первого) игрока.

2. Определяют нижнюю (верхнюю) границу выигрыша.

3. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой.

4. Определяют цену игры и оптимальные стратегии.

Рассмотрим решение игры графическим методом на примере.

Пример 4. Решить графически игру, заданную платежной матрицей .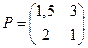

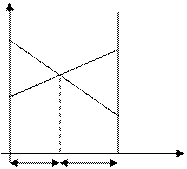Решение. Откладываем по оси абсцисс единичный отрезок А1А2. На вертикальной оси I – I откладываем отрезки: а₁₁= 1,5, соответствующий стратегии В1, и а₁₂ = 3, соответствующий стратегии В2. На вертикальной оси II – II отрезок а₂₁ =2 соответствует стратегии В1, а отрезок а₂₂ = 1 соответствует стратегии В2. Нижняя цена игры α = а₁₁ =1,5. Верхняя цена игры β = а₂₁ =2, седловая точка отсутствует.

Из рисунка видно, что абсцисса точки N определяет оптимальную стратегию игрока А, а ордината – цену игры ν. Точка N является точкой пересечения прямых В1В1 и В2В2. Уравнение прямой В1В1, проходящей через точку (0; 1,5) и (1; 2): у = 0,5х + 1,5.

Уравнение прямой В2В2, проходящей через точки (0; 3) и (1; 1): у = -2х +3.

Точка пересечения прямых является решением системы:

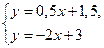
или х = 0,6; у = 1,8, т.е. N (0,6; 1,8).

Таким образом, u₁ = 0,6, u₂ = 1 – 0,6 = 0,4; оптимальная стратегия U*= (0,6; 0,4), цена игры ν = 1,8.

Геометрически также можно определить оптимальную стратегию игрока В, если поменять местами игроков А и В и вместо максимума нижней границы А2МА1 в соответствии с принципом минимакса рассмотреть минимум верхней границы.

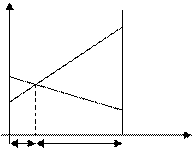Абсцисса точки М определяет оптимальную стратегию, а ордината этой точки – цена игры. Прямая А1А1, проходящая через точки (0; 1,5) и (1; 3), удовлетворяет уравнению

У =1,5х + 1,5

Прямая А2А2, проходящая через точки (0, 2) и (1; 1), удовлетворяет уравнению у = -х + 2.

Координаты точки пересечения М – это решение системы уравнений:

Откуда х=0,2; у=1,8, т.е.z₂=0,2; z₁=1-z₂=0,8. ν=1,8. Z*=(0,8;0,2). Оптимальное решение игры найдено.

3.

Поиск по сайту: