 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Приведение матричной игры к задаче линейного программирования
Рассмотрим игру mxn, определенную матрицей А = 
По теореме 3 для оптимальной стратегии первого игрока U*(u1*, u2*, …, um*) и цены игрока ν выполняется неравенство 
Пусть ν > 0. Разделим обе части неравенства на ν. 
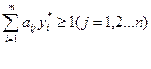 (*)
(*)
Из обозначения 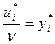 выразим ui*: ui* = ν * yi*. Т.к.
выразим ui*: ui* = ν * yi*. Т.к. 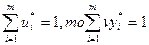 или
или  .
.
Т.к. первый игрок стремится получить максимальный выигрыш, то величина  должна быть минимальной, следовательно надо найти минимальной значение f* =
должна быть минимальной, следовательно надо найти минимальной значение f* =  при условии (*), т.е. если
при условии (*), т.е. если 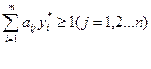 .
.
Аналогично рассуждая, можно получить, что оптимальная стратегия второго игрока сводится к нахождению максимального значения функции F =  при условиях
при условиях  .
.
Таким образом, чтобы найти решение игры, определенной матрицей А, надо составить пару двойственных задач на нахождение максимума и минимума соответствующих функций.
Прямая задача:
Найти максимум функции F =  при условиях
при условиях  .
.
Двойственная задача: Найти минимум функции f* =  , если
, если 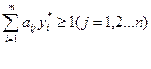 , уi ≥ 0 (i = 1, 2,.., m).
, уi ≥ 0 (i = 1, 2,.., m).
Итак, процесс нахождения решения игры включает следующие этапы:
1. Составить пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
2. Определить оптимальные решения пары двойственных задач.
3. Используя соотношение между решениями двойственных задач и оптимальными стратегиями и ценой игры, найти решение игры.
Пример. Найти решение игры определяемой матрицей А = 
Решение.
1. Составим двойственную пару задач линейного программирования. Прямая задача:
 х1 + 2х2 ≤ 1
х1 + 2х2 ≤ 1
х1 + х3 ≤ 1
2х1 + х2 ≤ 1
х1, х2, х3 ≥ 0
f = x1 + x2 + x3 → max
Обратная задача:
 у1 + у2 + 2у3 ≥ 1
у1 + у2 + 2у3 ≥ 1
2у1 + у3 ≥ 1
у2 ≥ 1
у1, у2, у3 ≥ 0
f = y1 + y2 + y3 → min
2. С помощью симплекс-метода определяются решения двойственных задач.

ui* = yi * ν, zi* = xi * ν => u*(1/2*2/3, 2/3,0) z* (0, 1/3, 2/3)
Задачи для самостоятельного решения.
- Для следующих платежных матриц определить верхнюю и нижнюю цену игры, минимаксные стратегии и оптимальные решения игры, если существует седловая точка.
 ;
; 
- Решить графическим методом игру, заданную матрицей

- Предприятие может выпускать три вида продукции (А1, А2, А3), получая при этом прибыль зависящую от спроса, который может быть в одном из следующих состояний (В1, В2, В3). Дана матрица (таблица), элементы которой aij характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м состоянием спроса. Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Поиск по сайту: