Оцененный пробег автомобиля (тыс. миль)

Рис. 4.5. Вариация и кривые распределения

В качестве меры вариации обычно принимается среднее квадратическое отклонение, которое характеризует среднее расстояние от средней оценки ответов каждого респондента на определенный вопрос. Можно сравнить среднее квадратическое отклонения для двух выборок и опреде­лить, для какой из них вариация является меньшей.

Поскольку все маркетинговые решения принимаются в условиях неопределенности, то это обстоятельство целесообразно учесть при опре­делении объема выборки. Так как определение исследуемых величин для совокупности в целом осуществляется на основе выборочной статистики, то следует установить диапазон (доверительный интервал), в который, как ожидается, попадут оценки для совокупности в целом, и ошибку их определения.

Понятие «доверительный интервал» — это диапазон, крайним точ­кам которого соответствует определенный процент определенных ответов на какой-то вопрос. Данное понятие тесно связано с понятием «среднее квадратическое отклонение изучаемого признака в генеральной совокуп­ности»: чем оно больше, тем шире должен быть доверительный интервал, чтобы включить в свой состав, например, 95% ответов.

Из свойств нормальной кривой распределения вытекает, что ко­нечные точки доверительного интервала, равного, скажем, 95%, опреде­ляются как произведение 1,96, называемого нормированным отклонени­ем, на среднее квадратическое отклонение. Числа 1,96 и 2,58.(для 99%-ного доверительного интервала) обозначаются как Z. Имеются таблицы «Значение интеграла вероятностей», которые дают возможность опреде­лить величины Z для различных доверительных интервалов. Доверитель­ный интервал, равный или 95%, или 99%, является стандартным при проведении маркетинговых исследований.

Например, проведено исследование числа визитов автовладельцев в сервисные мастерские за год. Доверительный интервал для среднего чис­ла визитов был рассчитан равным 5—7 визитам при 99%-ном уровне до­верительности. Это означает, что если появится возможность провести независимо 100 раз выборочные исследования, то для 99 средних значе­ний числа визитов попадут в диапазон от 5 до 7 визитов — другими сло­вами, 99% автовладельцев попадут в доверительный интервал.

Предположим, было проведено исследование для пятидесяти неза­висимых выборок. Средние оценки для этих выборок образовали нор­мальную кривую распределения, которая в данном случае называется выборочным распределением. Средняя оценка для совокупности в целом равна средней оценке кривой распределения. Понятие «выборочное рас­пределение» также рассматривается в качестве одного из базовых поня­тий теоретической концепции, лежащей в основе определения объема выборки.

Очевидно, что ни одна компания не проводит маркетинговых ис­следований, формируя 50 независимых выборок. Обычно используется только одна выборка. И математическая статистика дает возможность получить некую информацию о выборочном распределении, владея толь­ко данными о вариации единственной выборки.

Индикатором степени отличия оценки, истинной для совокупности в целом, от оценки, которая ожидается для типичной выборки, является средняя квадратическая ошибка (см. ниже). Например, исследуется мне­ние потребителей о новом продукте и заказчик данного исследования указал, что его устроит точность полученных результатов, равная ±5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25—35%. Причем чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.

Теперь, после знакомства с базовыми понятиями, определим объем выборки на основе расчета доверительного интервала. Исходной инфор­мацией, необходимой для реализации данного подхода, является: 1. Ве­личина вариации, которой, как считается, обладает совокупность. 2. Же­лаемая точность. 3. Уровень доверительности, которому должны удовле­творять результаты проводимого обследования.

Когда на заданный вопрос существует только два варианта ответа, выраженные в процентах (используется процентная мера), объем выбор­ки определяется по следующей формуле:

Таблица 4.15

Значение нормированного отклонения оценки (z) от среднего значения в зависимости от доверительной вероятности (α) полученного результата

Например, фирмой, выпускающей покрышки, проводится опрос автолюбителей. Целью обследования является определение процента ав­толюбителей, использующих радиальные покрышки, поэтому на вопрос: «Используете ли вы радиальные покрышки?» — возможно только два ответа: «Да» или «Нет» (шкала наименований). Если предположить, что совокупность автолюбителей обладает низким показателем вариации, то это означает, что почти каждый опрошенный использует радиальные покрышки. В этом случае может быть сформирована выборка достаточно малых размеров. В формуле (4.1) произведение pq выражает вариацию, свойственную совокупности.

Предположим, что 90% единиц совокупности используют радиаль­ные покрышки. Это означает, что рq = 900. Если принять, что показатель вариации выше (р = 70%), то рq = 2100.

Наибольшая вариация достигается в случае, когда половина сово­купности (50%) используют радиальные покрышки, а другая (50%) — не использует. В этом случае произведение рq достигает наибольшего значе­ния, равного 2500.

При проведении обследования следует указать точность получен­ных оценок. Скажем, было установлено, что 44% респондентов исполь­зуют радиальные покрышки. В этом случае результаты измерения жела­тельно представить в виде: «Процент автолюбителей, использующих ра­диальные покрышки, составляет 44% плюс-минус...%». Величину допус­тимой ошибки заранее совместно определяют заказчик исследования и исследователь.

Что касается уровня доверительности, то при проведении марке­тинговых исследований, как отмечалось выше, обычно рассматриваются только два его значения: 95% или 99%. Первому значению соответствует значение z = 1,96, второму — z = 2,58. Если выбирается уровень довери­тельности, равный 99%, то это говорит о том, что мы уверены на 99% (другими словами, доверительная вероятность равна 0,99) в том, что про­цент членов совокупности, попавших в диапазон ± е%, равен проценту членов выборки, попавших в тот же диапазон ошибки.

Принимая вариацию, равную 50%, точность, равную ± 10%, при 95%-ном уровне доверительности, рассчитаем размер выборки:

При уровне доверительности, равном 99%, и е = ±3% n = 1067.

При определении показателя вариации для определенной совокуп­ности прежде всего целесообразно провести предварительный качествен­ный анализ исследуемой совокупности, в первую очередь установить схожесть единиц совокупности в демографическом, социальном и других отношениях, представляющих интерес для исследователя. Возможно про­ведение пилотного исследования, использование результатов подобных исследований, проведенных в прошлом. При использовании процентной меры изменчивости принимается в расчет то обстоятельство, что макси­мальная изменчивость достигается для р = 50%, что является наихудшим случаем. К тому же этот показатель радикальным образом не влияет на объем выборки. Учитывается также мнение заказчика исследования об объеме выборки.

Возможно определение объема выборки на основе использования средних значений, а не процентных величин, как это делалось выше. Предположим, что выбран уровень доверительности, равный 95% (z=1,96), среднее квадратическое отклонение (s) рассчитано равным 100 и желаемая точность (погрешность) составляет ±10. Определение объема выборки (n):

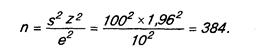
На практике, если выборка формируется заново и схожие опросы не проводились, то s не известно. В этом случае целесообразно задавать погрешность е в долях от среднеквадратического отклонения. Расчетная формула преобразуется и приобретает следующий вид:

Выше шел разговор о совокупностях очень больших размеров, ха­рактерных для рынков потребительских товаров. Однако в ряде случаев совокупности на являются столь большими — например, на рынках от­дельных видов продукции производственно-технического назначения.

Обычно, если выборка составляет менее пяти процентов от сово­купности, то совокупность считается большой и расчеты проводятся по вышеприведенным правилам.

Если же объем выборки превышает пять процентов от совокупно­сти, то последняя считается малой и в вышеприведенные формулы вво­дится поправочный коэффициент. Объем выборки в данном случае опре­деляется следующим образом:

где n' — объем выборки для малой совокупности;

n — объем выборки (или для процентных мер, или для средних), рас­считанный по приведенным выше формулам;

N — объем генеральной совокупности.

Например, изучается мнение членов совокупности, состоящей из 1000 компаний, относительно изменения местной налоговой политики органами власти определенного региона. Вследствие отсутствия инфор­мации о вариации принимается наихудший случай 50:50. Решено исполь­зовать уровень доверительности, равный 95%. Заказчик исследования заявил, что его устроит точность результатов ±5%. Тогда, используя фор­мулу для процентной меры, получим

Очевидно, что использование выборки меньших размеров приведет к экономии времени и средств.

Данный подход к определению объема выборки с известными ого­ворками может быть использован и при определении численности панели и экспертной группы (см. соответствующие разделы данной книги).

Приведенные формулы расчета объема выборки основаны на предположении, что все правила формирования выборки были соблюде­ны и единственной ошибкой выборки является ошибка, обусловленная ее объемом. Однако следует помнить, что объем выборки определяет точ­ность полученных результатов, но не их представительность. Последняя определяется методом формирования выборки. Все формулы для расчета объема выборки предполагают, что репрезентативность гарантируется использованием корректных вероятностных процедур формирования вы­борки.

Помимо четкого планирования репрезентативности выборки, нель­зя распространять полученные результаты за ее границы. Так, результаты исследования мнения массового потребителя города Москвы о товарах определенной фирмы нельзя распространять на всю Россию. Далее, можно быть поставленным в тупик разными результатами обследования степени лояльности потенциальных покупателей к определенной марке пылесоса (в одном исследовании была названа цифра 10%, в другом слу­чае — 25%). Дело в том, что в первом случае цифра была получена от общего числа опрошенных, а во втором случае — только от числа тех покупателей, которые твердо решили приобрести пылесос. Поэтому для вдумчивого маркетолога очень важными являются те пояснения, которые сопровождают социологические данные (как минимум, формулировки вопросов и описание выборки).

Поиск по сайту: