Індивідуальні завдання з теорії ймовірностей

Варіант індивідуального завдання з теорії ймовірностей визначається двома параметрами: 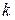– передостання цифра номера залікової книжки і – остання цифра номера залікової книжки. Завдання варіанта є на перетині відповідного рядка і стовпця:

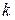
1. В ящику є 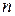кульок з яких 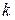білих і 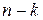чорних. Навмання беруть кульок. Знайти ймовірність того, що вони білі.

№					№

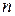
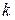
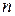
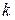
2. В партії з 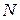виробів 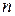пофарбованих. Навмання вибирають виробів. Знайти ймовірність того, що серед них є 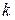пофарбованих.

№						№

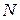
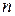
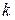
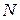
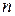
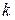
3. Ймовірності того, що потрібна формула є в першому, другому, третьому довіднику, відповідно дорівнюють 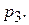Визначити ймовірності таких подій: 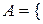формула є тільки в одному довіднику ; 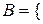формула є тільки в двох довідниках}; 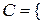формула є в усіх трьох довідниках}; формули нема в жодному довіднику ; формула є хоча б в одному довіднику .

№					№
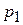
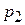
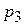
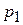
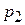
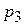
	0,2	0,5	0,9		0,3	0,7	0,8
	0,4	0,7	0,5		0,5	0,8	0,1
	0,6	0,7	0,8		0,6	0,9	0,3
	0,3	0,6	0,7		0,4	0,2	0,9
	0,1	0,8	0,5		0,7	0,8	0,2
	0,8	0,5	0,7		0,4	0,7	0,9
	0,4	0,9	0,8		0,5	0,2	0,1
	0,3	0,5	0,7		0,6	0,8	0,9
	0,8	0,1	0,9		0,2	0,3	0,7
	0,67	0,8	0,2		0,3	0,8	0,5

4. У лабораторії є 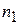комп’ютерів, виготовлених фір­мою A, 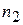комп’ютерів фірми B і 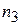комп’ютери фірми C. Ймовірності того, що комп’ютери, виготовлені цими фірмами, працюватимуть без ремонту протягом місяця, відповідно дорівнюють 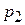і 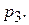Яка ймовірність того, що навмання вибраний комп’ютер працюватиме без ремонту протягом місяця? Навмання вибраний комп’ютер пропрацював без ремонту протягом місяця. Знайти ймовірність того, що це комп’ютер фірми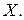

№
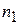
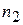
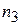
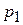
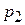
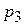
				0,25	0,74	0,36
				0,35	0,87	0,65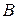
				0,26	0,32	0,75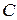
				0,33	0,56	0,91
				0,45	0,56	0,78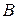
				0,47	0,36	0,87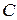
				0,38	0,69	0,93
				0,28	0,63	0,94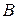
				0,58	0,73	0,67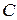
				0,35	0,85	0,92
				0,36	0,81	0,94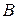
				0,22	0,47	0,68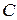
				0,66	0,86	0,91
				0,54	0,68	0,78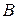
				0,72	0,83	0,95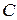
				0,46	0,59	0,81
				0,29	0,38	0,94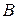
				0,33	0,96	0,95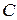
				0,94	0,88	0,65
				0,67	0,82	0,94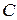

5. Ймовірність того, що електрична лампочка пропрацює протягом 5000 годин дорівнює 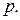Знайти ймовірність того, що з 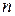лампочок протягом 5000 годин пропрацює а) лампочок; б) від до 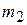лампочок; в) хоча б одна лампочка. Знайти найімовірнішу кількість лампочок, які пропрацюють протягом 2000 годин.

№
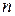
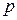
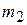
		0,7
		0,8
		0,7
		0,6
		0,8
		0,7
		0,8
		0,6
		0,9
		0,8
		0,7
		0,9
		0,6
		0,8
		0,9
		0,7
		0,8
		0,9
		0,8
		0,4

6. Ймовірність того, що електрична лампочка пропрацює протягом 5000 годин дорівнює 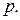Знайти ймовірність того, що з 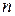лампочок протягом 5000 годин пропрацює а) лампочок; б) від до 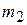лампочок.

№
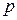
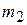
		0,7
		0,8
		0,7
		0,6
		0,8
		0,7
		0,8
		0,6
		0,9
		0,8
		0,7
		0,9
		0,6
		0,8
		0,9
		0,7
		0,8
		0,9
		0,8
		0,4

7. При скануванні тексту в середньому на кожну тисячу символів є 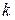помилкових. Знайти ймовірність того, що при скануванні тексту який має 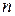символів буде помилкових.

№					№

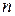
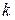
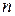
8. Торгова фірма має 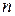баз. Ймовірність того, що на базі нема потрібного товару є однаковою і дорівнює 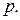Побудувати закон розподілу випадкової величини – кількості баз на яких нема потрібного товару.

№				№
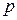
		0,2			0,25
		0,2			0,15
		0,1			0,35
		0,3			0,35
		0,3			0,12
		0,1			0,21
		0,1			0,22
		0,2			0.18
		0,3			0.14
		0,25			0.17

9. Задано закон розподілу випадкової величини 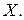Знайти 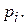Обчислити математичне сподівання і дисперсію цієї випадкової величини.

161.
	0,1		0,4	0,2
162.
		0,3	0,1	0,2
163.
	0,1	0,2		0,3
164.		–1
		0,3	0,4	0,2
165.		–2
	0,4	0,3	0,1
166.
		0,3	0,4	0,2
167.		–4	–3
	0,1		0,4	0,2
168.
	0,1	0,3		0,2
169.		–3	–2
	0,1	0,3	0,4
170.
	0,2	0,3		0,1
171.		–4	–2
	0,1		0,4	0,2
172.
		0,1	0,4	0,2
173.		–5	–2
	0,1		0,4	0,2
174.
	0,1	0,3		0,2
175.
	0,1	0,3	0,4
176.
	0,1	0,3		0,2
177.		–7	–2
	0,1		0,4	0,2
178.
	0,1	0,3	0,4	0,2
179.		–4	–2
		0,3	0,4	0,2
180.
	0,1	0,3	0,4	0,2

10. Задано функцію Потрібно: 1) знайти значення параметра 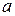при якому функція буде щільністю розподілу деякої випадкової величини 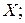2) обчислити дисперсію випадкової величини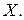

181.		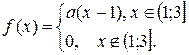	191.
182.			192.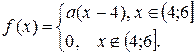
183.			193.
184.			194.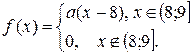
185.			195.
186.			196.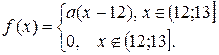
187.		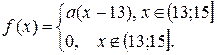	197.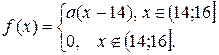
188.		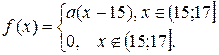	198.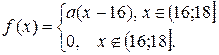
189.		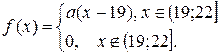	199.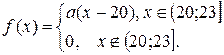
190.			200.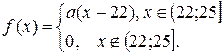

11. Задано математичне сподівання 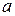та середнє квадратичне відхилення випадкової величини 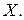Знайти: а) імовірність того, що випадкова величина набуде значення з інтервалу 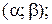б) ймовірність того, що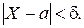

№

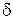
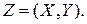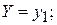12. Задано закон розподілу двовимірної випадкової величини Визначити: 1) безумовні закони розподілу складових; 2) умовний закон розподілу складової за умови, що складова набула значення 3) умовний закон розподілу за умови, що 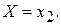Побудувати регресію випадкової складової на складову 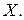Визначити коефіцієнти коваріації та кореляції між складовими та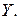

221.				231.
	0,16	0,1	0,28		0,21	0,07	0,23
	0,14	0,2	0,12		0,11	0,2	0,18

222.				232.
	0,12	0,13	0,24		0,15	0,23	0,15
	0,18	0,06	0,27		0,21	0,09	0,17

223.				233.
	0,16	0,1	0,28		0,21	0,07	0,23
	0,14	0,2	0,12		0,11	0,2	0,18

224.				234.
	0,12	0,13	0,24		0,15	0,23	0,15
	0,18	0,06	0,27		0,21	0,09	0,17

225.				235.
	0,16	0,1	0,28		0,21	0,07	0,23
	0,14	0,2	0,12		0,11	0,2	0,18

226.				236.
	0,12	0,13	0,24		0,15	0,23	0,15
	0,18	0,06	0,27		0,21	0,09	0,17

227.				237.
	0,16	0,1	0,28		0,21	0,07	0,23
	0,14	0,2	0,12		0,11	0,2	0,18

				238.
	0,12	0,13	0,24		0,15	0,23	0,15
	0,18	0,06	0,27		0,21	0,09	0,17

229.				239.
	0,16	0,1	0,28		0,21	0,07	0,23
	0,14	0,2	0,12		0,11	0,2	0,18

230.				240.
	0,12	0,13	0,24		0,15	0,23	0,15
	0,18	0,06	0,27		0,21	0,09	0,17

13. Задано закон розподілу випадкової величини 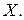За нерівністю Маркова оцінити ймовірність того, що випадкова величина набуде значення меншого ніж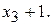

241.
	0,2	0,3	0,4	0,1

242.
	0,3	0,2	0,4	0,1

243.
	0,2	0,3	0,1	0,4

244.
	0,1	0,3	0,4	0,4

245.
	0,2	0,4	0,3	0,1

246.
	0,4	0,3	0,2	0,1

247.
	0,2	0,1	0,4	0,3

248.
	0,3	0,2	0,1	0,4

249.
	0,4	0,3	0,2	0,1

250.
	0,1	0,3	0,4	0,2

251.
	0,2	0,3	0,4	0,1

252.
	0,3	0,2	0,4	0,1

253.
	0,2	0,3	0,1	0,4

254.
	0,1	0,3	0,4	0,4

255.
	0,2	0,4	0,3	0,1

256.
	0,4	0,3	0,2	0,1

257.
	0,2	0,1	0,4	0,3

258.
	0,3	0,2	0,1	0,4

259.
	0,4	0,3	0,2	0,1

260.
	0,1	0,3	0,4	0,2

14. Задано закон розподілу випадкової величини 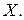За нерівністю Чебишева оцінити ймовірність того, що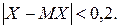

Поиск по сайту: