Тепловой взрыв в неадиабатических условиях

В реальных системах всегда происходят потери теплоты за счет теплопроводности через стенки, конвекции, излучения и т.д. При этом экзотермическая реакция будет либо ускоряться, приводя к взрыву, либо протекать с постоянной скоростью при постоянной температуре T = const, определяемой тепловым балансом системы. Так, в частности, протекают экзотермические реакции горения в газовых печах, котельных топках и других теплотехнических агрегатах.

При наличии тепловых потерь уравнение (2.2) примет вид

, (2.5)

где V – объем реактора;

S – площадь поверхности стенок реактора;

T_с – температура стенок реактора;

α – коэффициент теплопередачи.

Первое слагаемое в правой части уравнения (2.5) описывает скорость выделения тепла в системе за счет химической реакции. Второе слагаемое – скорость отвода тепла за счет теплопроводности стенок, которая линейно зависит от температуры реагирующей смеси. Скорость притока тепла растет по степенному закону с ростом начальной концентрации компонентов 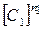, и экспоненциально растет с ростом температуры T в соответствии с законом Аррениуса.

Обозначим через . Графики зависимости скорости тепловыделения Q₊ и скорости теплопотерь Q_- от температуры Т приведены на рис. 2.8 для трех значений D:

D₁ > D_кр > D_2.

Из анализа приведенных графиков, которые представляют собой диаграмму Семенова, следует, что при D = D₁, кривые Q₊, Q_- не имеют точек пересечения; при D = D_кр, кривые Q₊, Q_- имеют одну точку касания; при D = D₂, кривые Q₊, Q_- имеют две точки пересечения.

В первом случае (D = D₁) скорость тепловыделения всегда превышает скорость теплопотерь, и в системе обязательно произойдет тепловой взрыв, так как температура смеси будет неограниченно возрастать.

Второй случай (D = D_кр), когда имеет место касание кривых тепловыделения и теплопотерь, определяет максимальное значение концентрации реагентов (параметра D), при котором скорость тепловыделения равна скорости теплопотерь.

Рис. 2.8. Влияние температуры неадиабатической системы на скорость тепловыделения и скорость теплопотерь

Все остальные кривые Q₊ для более низких значений концентрации реагентов пересекают кривую Q_- дважды. Причем, устойчивому состоянию системы отвечает только нижняя точка с более низкой температурой Т_уст.

Таким образом, если концентрация реагентов не превышает определенного критического для данной системы значения, то температура реагирующей смеси в реакторе будет постоянной T = Т_уст = const, причем Т_уст > Т_с. При выполнении этого условия после некоторого переходного периода в химическом реакторе устанавливается стационарный режим, при котором скорость экзотермической реакции будет иметь постоянное значение u = const.

На рис. 2.9 приведены три режима работы реактора в виде зависимости температуры от времени T = f(t).

Рис. 2.9. Режимы работы реактора

Температура Т₂ соответствует максимальной температуре в реакторе, при которой возможно устойчивое протекание химической реакции (при заданных значениях С₁, С₂, Т_с). Можно показать, что величина Т₂ определяется формулой

.

Температура Т₂ связана с параметрами реактора следующим соотношением:

.

Это уравнение позволяет определить взрывобезопасность каждого конкретного реактора.

Обозначим

Z₁ = ,

Z₂ = .

Если Z₂ << Z₁, то реактор взрывобезопасен, если Z₂» Z₁, то ситуация является критической, то есть можно ожидать взрыва; при Z₂ > Z₁ в реакторе обязательно произойдет тепловой взрыв.

Для расчета давления в реакторе по известной скорости роста температуры dT/dt используется уравнение состояния (уравнение Менделеева-Клапейрона)

,

где p, r, T, R – давление, плотность, абсолютная температура и газовая постоянная продуктов сгорания в реакторе. Газовая постоянная продуктов сгорания R рассчитывается по формуле

R = c_p – c_v,

где c_p, c_v – удельные теплоемкости продуктов сгорания при постоянном давлении и постоянном объеме, соответственно.

Поиск по сайту: