Примеры решения задач. Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct3, где А = 4 м, В = 2 м/c, С = 0,2 м/с3

Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct³, где А = 4 м, В = 2 м/c, С = 0,2 м/с³. Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указан­ные моменты времени; 4) среднее ускорение за указанный промежуток вре­мени; 5) мгно­венные ускорения в указанные моменты времени.

Дано:

x = A + Bt + Ct3 A = 4 м B = 2 м/c C = 0,2 м/c3 t1 = 2 c; t2 = 5 c	Решение 1. Чтобы найти координаты точки, надо в уравнение дви­же­­­ния подставить значения t1 и t2: x1 = (4+2×2+0,2×23) м = 9,6 м, x2 = (4+2×5+0,2×53) м = 39 м.
x1, x2, <u>-? u1, u2 -? <a>, a1, a2 -?	2. Средняя скорость ,

м/с = 9,8 м/с.

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:

u₁ = (2+3×0,2×2²) м/с = 4,4 м/c;

u₂ = (2+3×0,2×5²) м/с = 17 м/с.

4. Среднее ускорение ,

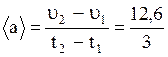м/c² = 4,2 м/с².

5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.

a₁ = 6×0,2×2 м/c² = 2,4 м/с²;

a₂ = 6×0,2×5 м/с² = 6 м/с².

Ответ: x₁ = 9,6 м; x₂ = 39 м; áuñ = 9,8 м/с; u₁ = 4,4 м/c; u₂ = 17 м/с; áаñ = 4,2 м/с²; a₁ = 2,4 м/с²; a₂ = 6 м/с².

Задача 2 Маховик вращается равноускоренно. Найти угол a, ко­то­рый составляет вектор полного ускорения 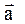любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.

Дано:

w0 = 0 N = 2 e = const	Решение Разложив вектор точки М на тангенци­аль­ное и нормальное уско­ре­ния, видим, что иско­мый угол определяется соотно­шением tga=at/an.
a -?

Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: a_t = eR, a_n = w²R, где R – радиус маховика, получим

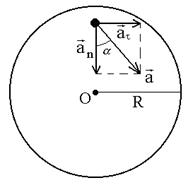tga =

так как маховик вращается равноускоренно, найдем связь между величинами e и w;

Поскольку w₀ = 0; j = 2pN, то w² = 2e×2pN = 4pNe.

Подставим это значение в формулу, получим:

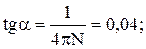a» 2,3°.

Ответ: a» 2,3°.

Задача 3 Две гири с массами m₁ = 2 кг и m₂ = 1 кг соединены нитью, пе­ре­ки­ну­той через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити . Трением в блоке пренебречь.

Дано:

m1 = 2 кг m2 = 1 кг	Решение Воспользуемся для решения задачи основным законом динамики где – равнодействующая всех сил, действующих на тело.
a, FН -?

На тело 1 и тело 2 действуют только две силы – сила тяжести и сила

натяжения нити. Для первого тела имеем

(1)

для второго тела

. (2)

Так как сила трения в блоке отсутствует,

.

Ускорения тел а₁ и а₂ направлены в противоположные стороны и равны по модулю:

.

Получаем из выражений (1) и (2) систему уравнений

Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений

в проекции на ось Х

Решая эту систему относительно а и F_Н, получаем:

= 3,3 м/с²; = 13 Н.

Ответ: a= 3,3 м/c²; F_H = 13 Н.

Задача 4 К ободу однородного диска радиусом R=0,2 м прило­жена каса­тель­ная сила F=98,1 Н. При вращении на диск действует момент сил трения

М_ТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с².

Дано:

R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c2	Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости: , где - момент сил, приложенных к телу,
m -?

относительно выбранной оси (M_F - момент силы F, M_тр – момент сил трения);

- момент инерции диска.

Учитывая, что M_F=F×R, получаем .

Отсюда ; m = 7,4 кг.

Ответ: m = 7,4 кг.

Поиск по сайту: