Молекулярно-кинетическая теория идеальных газов

1.1. Уравнение состояния

В состоянии термодинамического равновесия объем V, давление Р и температура Т находятся в функциональной зависимости, которую можно выразить уравнением

F (P,V,T) = 0.

Это соотношение называется уравнением состояния тела (системы). Вид функции F(P,V,T) различен для разных тел и точно установлен только в одном случае, а именно для идеального газа. Идеальным называется газ, в котором

,

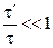где t^¢ - среднее время столкновения частиц, t - среднее время свободного пробега частиц. При этом средняя длина свободного пробега частиц должна быть много меньше размеров сосуда, в котором заключен газ. Данные условия выполняются достаточно хорошо для газов, молекулы которых имеют простое строение даже при давлениях, близких к атмосферному.

Уравнение состояния идеального газа можно получить, рассмотрев давление, создаваемое газом на стенку сосуда. Оно возникает в результате передачи импульса участку стенки при столкновениях с ним молекул газа. Учитывая, что в равновесном состоянии соударения молекул в среднем носят упругий характер, давление идеального газа оказывается пропорциональным средней энергии поступательного движения частиц, заключенных в единице объема:

,

где n – плотность (концентрация) частиц, n = N/V, N – число частиц.

Используя связь кинетической энергии молекул и температуры, получаем

P = nkT.

Существует несколько форм записи этого уравнения:

PV = NkT;

PV = 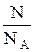N_AkT = nRT,

где n = 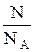– количество вещества, R = N_A×k = 8,31 Дж/(моль×К) – универсальная газовая постоянная. Используя выражение для количества вещества через массу и молярную массу газа можно получить известное уравнение Клапейрона – Менделеева

PV = 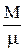RT,

где М – масса газа, m – молярная масса газа.

Из последнего уравнения состояния можно получить известный закон Дальтона и уравнения изопроцессов:

а) давление механической смеси газов равно сумме парциальных давлений газов, входящих в смесь:

PV = (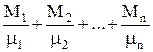)RT;

б) изотермический процесс – Т=const, PV = const, P₁V₁ = P₂V₂;

изобарический процесс – P = const, ;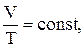

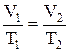изохорический процесс – V = const, .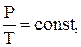

1.2. Уравнение состояния Ван-дер-Ваальса

При увеличении плотности (давления) поведение газа все сильнее отличается от поведения идеального газа. Это объясняется тем, что при малых средних расстояниях между молекулами все большее значение приобретают силы межмолекулярного взаимодействия. На малых расстояниях эти силы являются силами отталкивания, а на больших – силами притяжения. Влияние этих сил на вид уравнения состояния можно приближенно учесть следующим образом. Для реальных газов давление должно резко возрастать при конечном объеме, равном по порядку величины объему всех частиц газа. Обозначим этот конечный объем для одного моля через b, тогда давление газа может быть записано в виде

.

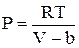Действие сил притяжения между молекулами проявляется в уменьшении давления газа по сравнению с приведенной величиной. Уменьшение давления связано с тем, что на молекулу, находящуюся у стенки сосуда, действует сила, направленная внутрь сосуда. Она обусловлена притяжением со стороны молекул газа, находящихся в его объеме. В первом приближении ее величина пропорциональна концентрации молекул n = , а, учитывая, что давление само пропорционально концентрации, поправка на уменьшение давления будет пропорциональна n² = 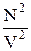. Учитывая это, можно прийти к соотношению

P = ,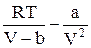

которое в форме называется уравнением Ван-дер-Ваальса (для одного моля газа). Поправки a и b – постоянные Ван-дер-Ваальса, учитывающие соответственно действие сил притяжения и отталкивания между молекулами газа.

1.3. Внутренняя энергия

Важной характеристикой состояния системы является ее внутренняя энергия. Она определяется как среднее значение полной энергии ее частиц. Во внутренней энергии можно выделить следующие составляющие:

- энергия поступательного, вращательного и колебательного движений атомов и молекул;

- энергия межмолекулярного взаимодействия;

- энергия связи атомов в молекулах (химическая энергия);

- энергия связи электронов в атомах;

- энергия связи атомных ядер и др.

При различных процессах в системе изменяется внутренняя энергия. Как правило, это происходит из-за изменения одной или нескольких составляющих внутренней энергии, поэтому и в самой внутренней энергии следует учитывать только те составляющие, которые изменяются в ходе процесса. Отметим общие свойства внутренней энергии:

- в состоянии теплового равновесия движение частиц системы таково, что в любой момент времени полная энергия частиц с высокой степенью точности равна внутренней энергии (статистические флуктуации очень малы);

- внутренняя энергия системы является функцией ее термодинамических параметров;

- внутренняя энергия обладает свойством аддитивности, т.е. внутренняя энергия системы равна сумме внутренних энергий частей (макроскопических), составляющих данную систему.

Определим внутреннюю энергию идеального газа в равновесном состоянии – это энергия поступательного, вращательного и колебательного движений атомов и молекул. Поступательное движение частиц газа носит классический характер, а вращательное и колебательное движение – квантовый, т.е. такие движения возникают только про сообщении молекулам конечной порции энергии DЕ. Для большинства газов DЕ^кол~ 10^-20Дж, что соответствует температуре Т^кол ~10³ К, DЕ^вр~10^-21 Дж, а температура Т^вр ~10 К. Общая закономерность квантовых движений следующая: с ростом температуры квантовое движение быстро приобретает классический характер. Поэтому при обычных условиях можно движение молекул считать классическим и для вычисления внутренней энергии воспользоваться законом равнораспределения энергии по классическим степеням свободы: «В состо­янии теплового равновесия на каждую поступательную и вращательную степень свободы приходится в среднем энергия, равная кТ/2, а на колебательную – кТ».

Числом степеней свободы называется минимальное количество координат, однозначно определяющих положение тела (системы) в пространстве, или количество независимых движений, благодаря которым тело обладает энергией. В атомарном газе каждый атом имеет три поступательных степени свободы, в газе с двухатомными молекулами каждая молекула имеет три поступательных и две вращательных степени свободы, в газе с многоатомными молекулами, в общем случае, - три поступательных и три вращательных. Тогда внутренняя энергия газ имеет вид

U = N = ,

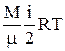где i – число степеней свободы молекул газа.

1.4. Статистические распределения

При тепловом движении положения частиц, величина и направление их скоростей изменяются случайным образом. Вследствие гигантского числа частиц случайный характер их движения, проявляется в существовании определенных статистических закономерностей в распределении частиц системы по координатам, значениям скоростей и т.д. Подобные распределения характеризуются соответствующими функциями распределения. Функция распределения (плотность вероятности) характеризует распределения частиц по соответствующей переменной (координаты, величины скоростей и т.д). В основе классической статистики лежат следующие положения:

- все частицы классической системы различимы (т.е. их можно пронумеровать и следить за каждой частицей);

- все динамические переменные, характеризующие состояние частицы, изменяются непрерывно;

- в заданном состоянии может находиться неограниченное число частиц.

1.4.1. Распределение Максвелла

В состоянии теплового равновесия как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул в газе, при Т=cоnst, остается постоянной и равной 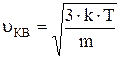. Это объясняется тем, что в газе устанавливается некоторое стационарное статистическое распределение молекул по значениям скоростей, называемое распределением Максвелла. Распределение Максвелла описывается некоторой функцией f(u), называемой функ­ци­ей распределения молекул по скоростям.

,

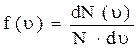где N – общее число молекул, dN(u) – число молекул, скорости которых принадлежат интервалу скоростей от u до u + du.

Таким образом, функция Максвелла f(u) равна вероятности того, что величина скорости наугад выбранной молекулы принадлежит единичному интервалу скоростей вблизи значения u. Или она равна доле молекул, скорости которых принадлежат единичному интервалу скоростей вблизи значения u.

Явный вид функции f(u) был получен теоретически Максвеллом:

.

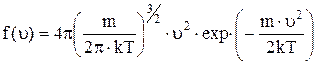График функции распределения приведен на рис. 12. Из графика следует, что функция распределения стремится к нулю при u®0 и u®¥ и проходит через максимум при некоторой скорости u_В, называемой наиболее вероятной скоростью. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно u_В. Значение наиболее вероятной скорости можно найти, используя условие для максимума функции f(u).

.

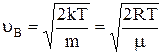На рис. 13 показано смещение u_В с изменением температуры, при этом площадь под графиком остается постоянной и равной 1, что следует из условия нормировки функции Максвелла

.

Условие нормировки следует из смысла данного интеграла – он определяет вероятность того, что скорость молекулы попадает в интервал скоростей от 0 до ¥. Это достоверное событие, его вероятность, по определению, принимается равной 1.

Знание функции распределения молекул газа по скоростям позволяет вычислять средние значения любых функций скорости, в частности средней арифметической скорости <u>.

.

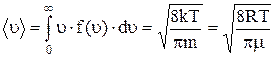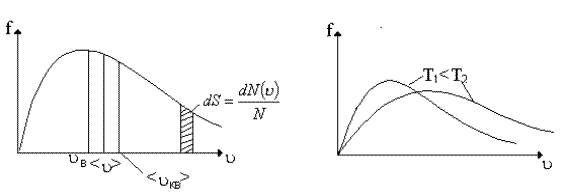
Рис.12 Рис. 13

По функции Максвелла можно определить долю молекул, скорости которых принадлежат заданному интервалу скоростей или превышают некоторое значение скорости, например вторую космическую, что определяет рассеяние атмосферы.

.

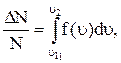
1.4.2. Распределение Больцмана

Тепловое движение частиц тела приводит к тому, что положение их в пространстве изменяется случайным образом. Поэтому можно ввести функцию распределения частиц по координатам, определяющую вероятность обнаружения частицы в том или ином месте пространства.

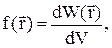
где 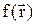- плотность вероятности, т.е. вероятность обнаружения частицы в единичном объеме вблизи точки с радиус-вектором .

При отсутствии внешних силовых полей существует равномерное распределение частиц идеального газа по координатам, при этом можно записать

,

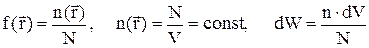где n - концентрация частиц, N - полное число частиц газа.

Внешнее силовое поле изменяет пространственное распределение частиц, при этом концентрация частиц и функция распределения зависят от координат. Если внешнее силовое поле является потенциальным, то концентрация частиц вблизи точки пространства с радиусом-вектором зависит от потенциальной энергии частиц в данном месте:

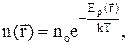
где n_o - концентрация частиц в том месте, где E_p=0.

В этом случае вероятность обнаружить частицу в объеме dV вблизи точки с радиусом-вектором определяется выражением

.

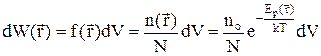Этот закон называется распределением Больцмана.

Для идеального газа давление связано с концентрацией соотношением Р=nkT. В поле земного тяготения концентрация изменяется с высотой над поверхностью Земли, и если газ находится в равновесном состоянии при температуре Т, то изменение давления с высотой происходит по закону

.

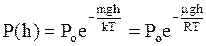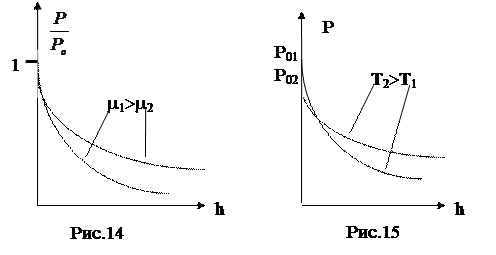
Последнее соотношение называется барометрической формулой. В действительности земная атмосфера не находится в равновесном состоянии, ее температура меняется с высотой, и барометрическую формулу следует применять к участкам атмосферы, в пределах которых изменением температуры можно пренебречь. Из барометрической формулы следует, что давление различных газов изменяется с высотой по-разному. На рис. 14 показано изменение давления газа с высотой для различных газов при T = const, а на рис. 15 – изменение давления газа (m = const) при разных темпе­ра­ту­рах.

1.5. Среднее число столкновений и средняя длина свободного пробега молекул

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Расстояния, которые проходят молекулы между двумя последовательными столкновениями, изменяются случайным образом. Поэтому можно говорить о средней длине свободного пробега молекул <l>.

Минимальное расстояние, на которое сближаются центры молекул, называется эффективным диаметром молекулы d. Он зависит от скорости сталкивающихся молекул, т.е. от температуры. За 1 с молекула проходит путь, равный <u>, и если <z> - среднее число столкновений за единицу времени, то .

Движущаяся молекула (рис. 16), сталкивается только с теми молекулами, центры которых находятся внутри цилиндра радиусом 2r=d.

,

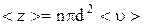более точно 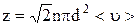- при учете движения других молекул.

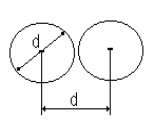
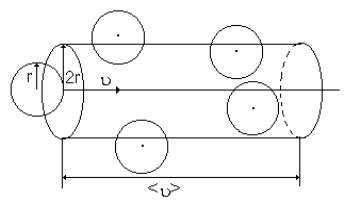
Рис. 16

.

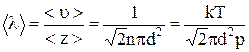1.6. Явления переноса в газах

В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса. В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движения (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным. В противном случае - это нестационарный процесс. Стационарные процессы возможны только в стационарных внешних условиях. В термодинамически изолированной системе могут возникать только нестационарные явления переноса, направленные на установление равновесного состояния.

Диффузия, теплопроводность, вязкость являются необратимыми процессами, возникающими самопроизвольно вследствие теплового движения при отклонении вещества (газа) от равновесного состояния. Это отклонение заключается в неоднородном распределении вещества, его температуры, в различии скоростей направленного движения макроскопических частей среды.

Диффузия

Под диффузией обычно понимается взаимопроникновение вещества в различных смесях, сопровождающееся направленным переносом массы вещества из мест с высокой плотностью в места с меньшей плотностью. Перенос массы вещества подчиняется закону Фика: «Плотность потока вещества (масса, переносимая за единицу времени через единичную площадку) прямо пропорциональна градиенту плотности»:

где D – коэффициент диффузии. Знак минус показывает, что перенос массы происходит в направлении убывания плотности.

Масса вещества, перенесенная в результате стационарной диффузии через площадь S за время t:

.

Согласно кинетической теории газов,

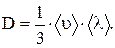
Теплопроводность

Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул температура выравнивается. Процесс передачи энергии в форме тепла подчиняется закону Фурье: «Плотность потока тепла (количество теплоты, переносимое за единицу времени через единичную площадку) прямо пропорционально градиенту температуры»:

,

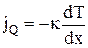где k - коэффициент теплопроводности. Знак минус показывает, что при теплопроводности энергия переносится в сторону убывания температуры. Количество тепла, переносимое в стационарном процессе теплопроводности (стационарное пространственное распределение температуры) через площадь S за время t:

.

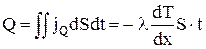Для идеального газа 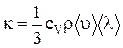, где c_v – удельная теплоемкость газа при постоянном объеме, r - плотность газа.

Вязкость

Вязкое трение в газе или жидкости - это результат переноса импульса направленного движения. Механизм возникновения внутреннего трения между слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к появлению сил вязкого трения. Внутреннее трение подчиняется закону Ньютона: «Плотность потока импульса направленного движения (равная силе вязкого трения, действующей на единичную площадку, перпендикулярную направлению переноса) пропорциональна градиенту скорости направленного движения»:

,

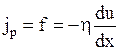где h - динамическая вязкость (коэффициент вязкости), 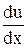- градиент скорости направленного движения. Знак минус указывает, что сила трения направлена против скорости u. Коэффициент вязкости для идеального газа

.

Сила F, действующая на площадь S, пропорциональна этой площади и градиенту скорости :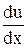

.

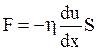Коэффициенты переноса связаны между собой простыми соотношениями

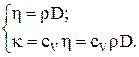
2. Основы термодинамики

2.1. Первое начало термодинамики

Внутренняя энергия макроскопической системы качественно отличается от механической энергии частиц, образующих систему. Это проявляется в существовании двух форм изменения внутренней энергии – работы и теплопередачи (теплообмена). Работа совершается в тех случаях, когда при взаимодействии системы с окружающими телами возникает какое-либо упорядоченное движение. В частности, газ совершает работу только при изменении его объема. В процессе теплопередачи также может происходить изменение внутренней энергии, обусловленное изменением энергии частиц, образующих систему, и не связанное с совершением работы. Изменение внутренней энергии в этом случае измеряется количеством тепла.

Закон сохранения энергии, в котором учитывается особая форма передачи энергии путем теплопередачи, является фундаментальным законом физики и называется первым началом термодинамики: «Количество тепла, полученное системой, расходуется на приращение внутренней энергии системы и на совершение системой работы над внешними телами (системами)».

Первое начало сформулировано на основании обобщения опытных фактов и справедливо для всех тепловых процессов. Последнее соотношение является термодинамическим определением внутренней энергии системы.

«Внутренняя энергия системы является функцией ее состояния, определенной с точностью до произвольной постоянной, приращение которой равно разности между количеством тепла, полученным системой, и работой, совершенной системой в ходе теплового процесса».

Изменение внутренней энергии зависит только от начального и конечного состояний системы. Работа и количество тепла зависят от вида процесса, переводящего систему из начального состояния в конечное, т.е. они не являются функциями состояния системы.

Если система периодически возвращается в первоначальное состояние, то DU=0 и A=Q, т.е. нельзя построить вечный двигатель, который совершал бы большую по величине работу, чем количество сообщенной ему извне энергии.

По форме обмена энергией можно выделить три вида систем:

1) изолированные (dQ=0, dA=0),

2) теплоизолированные (адиабатические) (dQ=0, dA¹0),

3) тепловые резервуары (dA=0, dQ¹0).

2.2. Работа газа при изменении его объема

Найдем работу, совершаемую газом при изменении его объема. Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде (рис. 17).

Если газ, расширяясь, передвигает поршень на расстояние dx, то он производит работу против сил внешнего давления р_е:

,

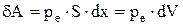где S - площадь поршня, dV - изменение объема газа. Полная работа А₁₂, совершаемая газом при изменении его объема от V₁ до V₂:

.

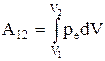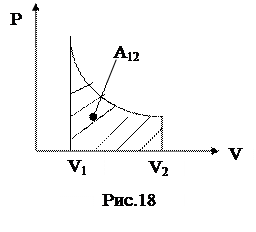
Если процесс расширения газа является равновесным, т.е. идущим без перепадов давлений и температур, то работа может быть вычислена через давление самого газа (р_е=р). Графически работа газа равна площади под кривой процесса на диаграмме PV (рис.18). Если газ совершает круговой процесс (цикл), то работа будет равна площади цикла.

Работа газа при изопроцессах:

1) изохорический V=const, dV=0, A₁₂=0;

2) изотермический T=const, ;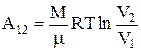

3) изобарический р=const,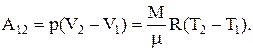

2.3. Теплоемкость

Теплоемкость тела или системы - скалярная физическая величина, характеризующая процесс теплообмена и равная количеству тела, полученному системой при изменении его температуры на один кельвин.

Теплоемкость можно отнести к одному молю или к единице массы вещества. Соответствующие теплоемкости называются молярной С_m или удельной с. Единицами измерения теплоемкостей являются: Дж/К (полная теплоемкость), Дж/(моль×К) (молярная теплоемкость), Дж/(кг×К) (удельная теплоемкость). Зная теплоемкости, можно вычислить количество тепла, полученное системой:

Q=CDT, Q=nC_mDT, Q=cMDT.

Теплоемкость, как и количество тепла, зависит от вида теплового процесса. Различают теплоемкости при постоянном давлении и постоянном объеме, если в процессе нагревания вещества поддерживаются постоянными соответственно давление и объем. Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщенная газу извне теплота идет на увеличение его внутренней энергии:

.

Используя первое начало термодинамики, можно показать, что молярная теплоемкость газа при постоянном объеме C_mVи молярная теплоемкость газа при постоянном давлении C_mPсвязаны соотношением 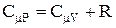. Это соотношение называется уравнением Майера.

При рассмотрении тепловых процессов важно знать характерное для каждого газа отношение C_mP к C_mV, которое называется показатель адиабаты или коэффициент Пуассона:

Из последних формул следует, что молярные теплоемкости не зависят от температуры в тех областях, где g = const.

2.4. Применение первого начала термодинамики к изопроцессам

Изохорический процесс (V = const). Газ не совершает рабо­ту, т.е. dA=0. Из первого начала термодинамики следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

.

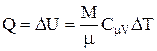Изобарический процесс (p = const). Теплота, сообщаемая газу, идет на приращение внутренней энергии и на совершение работы над внешними телами:

.

Изотермический процесс (T = const). Внутренняя энергия газа не изменяется и все количество тепла, сообщаемое газу, расходуется на совершение им работы против внешних сил:

.

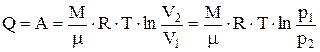2.5. Адиабатический процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен
(dQ = 0) между физической системой и окружающей средой. Близкими к адиа­ба­ти­ческим являются все быстропротекающие процессы. Из первого начала термодинамики для адиабатического процесса следует, что , т.е. работа совершается за счет убыли внутренней энергии системы. Используя первое начало термодинамики, можно получить уравнения адиабатического процесса:

;

.

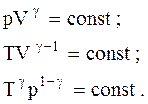Вычислим работу, совершаемую газом в адиабатическом процессе. Если газ расширяется от объема V₁ до V₂, то его температура падает от T₁ до T₂ и работа расширения идеального газа

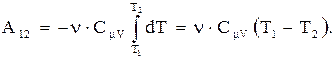
Это выражение для работы при адиабатическом процессе можно преобразовать к виду

.

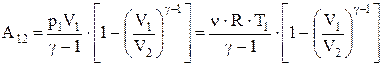2.6. Обратимые и необратимые процессы. Коэффициент полезного действия теплового двигателя

К обратимым процессам относятся процессы, после проведения которых в прямом и обратном направлениях в окружающих систему телах не остается никаких изменений. Для обратимых процессов характерно следующее: если в ходе прямого процесса система получила количество тепла Q и совершила работу А, то в ходе обратного процесса система отдает количество тепла Q^¢ = -Q и над ней совершается работа А^¢ = -А. К обратимым процессам относятся все равновесные процессы. В случае необратимого процесса, после возвращения системы в исходное состояние, в окружающих систему телах остаются изменения (изменяются положения тел и их температуры). Все реальные процессы в большей или меньшей степени необратимы.

В процессе преобразования тепла в работу используется тепловой двигатель, работающий по какому-либо круговому процессу (циклу). Коэффициент полезного действия такого двигателя (термический КПД) определяет долю тепла, превращаемую в работу:

,

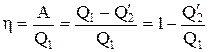где А - работа, совершенная двигателем за цикл, Q₁ - количество тепла, полученного двигателем, Q^¢₂ - количество тепла, отданного двигателем в окружающую среду. Работу теплового двигателя можно представить на диаграмме состояний в виде некоторого теплового кругового процесса (рис.19). Общая работа А определяется площадью цикла 1а2в1. Если за цикл совершается А>0, то цикл называется прямым, и если А<0, – обратным.

Прямой цикл используется в тепловом двигателе, совершающем работу за счет получения извне теплоты. Обратный цикл используется в холодильных машинах, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой (рис. 20).

Важной задачей термодинамики является изучение процессов преобразования тепла в работу и установления возможных границ повышения термического КПД.

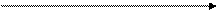
2.7. Второе начало термодинамики

Анализ выражения для КПД показывает, что максимальный КПД, равный единице, возможен, если двигатель все получаемое количество тепла будет преобразовывать в работу. Все опытные факты свидетельствуют о невозможности создания такого двигателя (вечный двигатель второго рода), и это было сформулировано в виде второго начала термодинамики.

«Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара».

Вильям Томсон (лорд Кельвин).

«Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому».

Рудольф Клаузиус.

Второе начало термодинамики не только установило границы преобразования тепла в работу, но и позволило построить рациональную шкалу температур (термодинамическая шкала температур) и установить направление процессов, происходящих в теплоизолированных системах.

2.8. Цикл Карно и теорема Карно

В 1824 г. С. Карно предложил и исследовал идеальный тепловой цикл, названный в последствии циклом Карно. Этот цикл состоит из двух изотерм и двух адиабат (рис. 21). Карно также сформулировал две теоремы, определяющие максимальное значение КПД теплового двигателя.

«Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т₁ и Т₂ нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества».

«Коэффициент полезного действия всякой тепловой машины не может превосходить коэффициента полезного действия идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника».

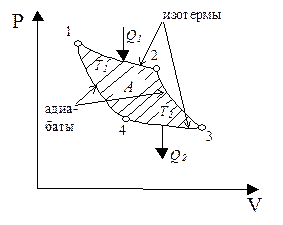Рис. 21

1®2, 3®4, – изотермические расширение и сжатие, 2®3, 4®1– адиабатические расширение и сжатие. В процессе 1®2 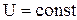, поэтому Q1 = 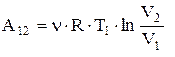. В процессе 3®4 U = const, поэтому .

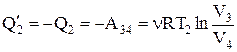Используя уравнения для адиабатического процесса можно показать, что 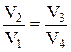. Тогда

.

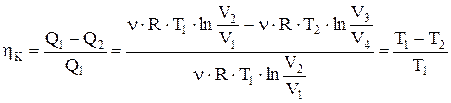2.9. Термодинамическое неравенство Клаузиуса. Энтропия

Рассматривая процессы превращения тепла в работу, Р. Клаузиус сформулировал термодинамическое неравенство (неравенство Клаузиуса): «Приведенное количество тепла, полученное системой в ходе произвольного кругового процесса, не может быть больше нуля».

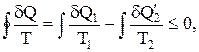
где dQ – количество тепла, полученное системой при температуре Т, dQ₁ - количество тепла, получаемое системой от участков окружающей среды с температурой Т₁, dQ^¢₂ – количество тепла, отдаваемое системой участкам окружающей среды при температуре Т₂. Неравенство Клаузиуса позволяет установить верхний предел термического КПД при переменных температурах нагревателя и холодильника.

,

где Т_{1 макс} – максимальная температура участка среды, от которого система получает тепло; Т_{2 мин} – минимальная температура участка среды, которому система отдает тепло.

Из выражения для обратимого цикла Карно следует, что или 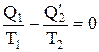, т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученное системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией.

Энтропия системы – функция ее состояния, определенная с точностью до произвольной постоянной. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.

, .

Важной особенностью энтропии является ее возрастание в изолированных системах (закон возрастания энтропии): «Энтропия теплоизолированной (адиабатической) системы не может убывать; она возрастает, если в системе идет необратимый процесс, и остается постоянной при обратимом процессе в системе».

Необратимые процессы в системе приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума и в дальнейшем никакие макроскопические процессы в системе невозможны.

Изменение энтропии при наличии теплообмена с окружающей средой, может быть каким угодно: как больше нуля, так и меньше нуля.

Получим выражение для приращения энтропии идеального газа при переходе из состояния с параметрами T₁, V₁ в состояние с параметрами T₂, V₂:

.

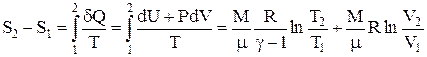Из выражения для приращения энтропии газа следует, что энтропия является функцией двух параметров - температуры и объема S=S(T,V).

Введение энтропии позволяет объединить первое и второе начала термодинамики в виде термодинамического неравенства

,

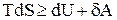где знак равенства относится к обратимым процессам, знак неравенства - к необратимым. Энтропия, как и внутренняя энергия, связана с микроскопическим строением системы и статистическим характером теплового движения частиц системы.

2.10. Фазовое пространство. Микро- и макросостояния системы

Статистический анализ поведения системы свидетельствует о том, что вероятность состояния и энтропия ведут себя схожим образом, а именно: при переходе системы к равновесному состоянию и энтропия, и вероятность возрастают. Для установления точного соотношения между ними необходимо ввести статистическое описание системы с микроскопической и макроскопической точек зрения. Это возможно путем введения фазового пространства, в котором движутся частицы системы. Фазовое пространство – шестимерное пространство, по осям которого откладываются значения координат и проекций импульсов частиц (x, y, z, p_x, p_y, p_z). Учитывая, что динамические переменные изменяются непрерывно, вести описание состояний с указанием точных значений координат и импульсов для каждой частицы невозможно. Поэтому все фазовое пространство разбивается на фазовые ячейки объемом DV=Dx×Dy×Dz×Dp_x×Dp_y×Dp_z. Теперь состояние каждой частицы может быть определено указанием того, в какой фазовой ячейке она находится. Состояние системы, заданное указанием того, какие частицы находятся в каждой фазовой ячейке, называется микросостоянием системы.

С макроскопической точки зрения состояние системы зависит от того, сколько частиц имеют то или иное значение энергии или сколько частиц находится вблизи данной точки системы, но не какие именно это частицы. Поэтому состояние системы, заданное указанием того, сколько частиц находится в каждой фазовой ячейке, называется макросостоянием системы.

При подобном описании состояния системы перемещения частиц в пределах фазовой ячейки не изменяют ни микро- ни макросостояние. Переходы частиц из одной ячейки в другую при неизменном их числе в каждой фазовой ячейке изменяют микросостояние, но оставляют прежнее макросостояние. Таким образом, одно и то же макроскопическое состояние может быть реализовано при самых различных микросостояниях. Это приводит к тому, что вероятность возникновения того или иного макросостояния системы зависит от числа микросостояний, реализующих данное макросостояние.

2.11. Статистический вес (термодинамическая вероятность) макросостояния и его связь с энтропией

Количество различных микросостояний, реализующих данное макросостояние системы, называется статистическим весом или термодинамической вероятностью макросостояния.

Все микросостояния системы равновероятны, а вероятность (математическая) макросостояния определяется ее статистическим весом. Анализ значений статистических весов различных макросостояний показывает, что в равновесном состоянии статистический вес максимален. Это означает, что все макроскопические процессы обладают односторонней направленностью. Переход между двумя макроскопическими состояниями возможен только в том случае, если конечное состояние является более вероятным, чем начальное. В этом заключается механизм необратимости тепловых процессов, которая проявляется в стремлении всех макроскопических тел перейти в равновесное состояние. С другой стороны, статистика не исключает самопроизвольных переходов в неравновесные состояния, просто эти переходы маловероятны (статистические флуктуации).

Получим выражение для статистического веса макросостояния. Пусть в системе имеется N частиц, а все фазовое пространство (область возможных значений координат и импульсов) разбито на m ячеек. Рассчитаем статистический вес состояния, при котором: в 1^ой ячейке находится N₁ частиц; во 2^ой ячейке – N₂ частиц и т.д.; в m^ой ячейке - N_m частиц. Для этого достаточно рассчитать число возможных перестановок частиц между ячейкам (они не изменяют числа частиц в ячейках). Это можно сделать, если из общего числа перестановок N частиц N! исключить перестановки в пределах каждой ячейки N_i! (они ничего не изменяют).

.

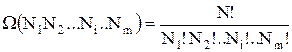Если в системе создать искусственно неравновесное состояние, то в подавляющем большинстве случаев система самопроизвольно будет переходить в состояние с большей вероятностью. С другой стороны, согласно термодинамике, все самопроизвольные процессы в замкнутой системе сопровождаются возрастанием энтропии. Поэтому следует ожидать, что между энтропией системы S в каждом состоянии и вероятностью W того же состояния должна существовать однозначная связь. Эта связь была установлена Больцманом (формула Больцмана):

,

где k – постоянная Больцмана.

Последнее соотношение можно рассматривать как определение энтропии. При таком понимании энтропии закон ее возрастания утрачивает свою абсолютность и становится статистическим законом. Энтропия замкнутой системы может не только возрастать, но и убывать. Это можно трактовать следующим образом: если система находится в неравновесном состоянии, то переход ее в более вероятное состояние будет происходить в подавляющем большинстве случаев, переходы же в менее вероятные состояния (с меньшей энтропией) настолько маловероятные, что практически не имеют никакого значения. Тогда закон возрастания энтропии оправдывается на практике с абсолютной достоверностью.

Поиск по сайту: