Законы Ньютона. Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения

Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния.

Тела, не подверженные внешним воздействиям, называются свободными телами. Система отсчёта, связанная со свободным телом, называется инерциальной системой отсчёта (ИСО). По отношению к ней любое свободное тело будет двигаться равномерно и прямолинейно или находиться в состоянии покоя. Из относительности движения следует, что система отсчёта, движущаяся равномерно и прямолинейно по отношению к ИСО, также является ИСО. ИСО играют важную роль во всех разделах физики. Это связано с принципом относительности Эйнштейна, согласно которому математическая форма любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчёта.

К основным понятиям, используемым в динамике поступательного движения, относятся сила, масса тела, импульс тела (системы тел).

Силой называется векторная физическая величина, являющаяся мерой механического действия одного тела на другое. Механическое действие возникает как при непосредственном контакте взаимодействующих тел (трение, реакция опоры, вес и т.д.), так и посредством силового поля, существующего в пространстве (сила тяжести, кулоновские силы и т.д.). Сила характеризуется модулем, направлением и точкой приложения.

Одновременное действие на тело нескольких сил , ,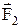..., может быть заменено действием результирующей (равнодействующей) силы :

= + +...+ = .

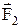Массой тела называется скалярная величина, являющаяся мерой инертности тела. Под инертностью понимается свойство материальных тел сохранять свою скорость неизменной в отсутствие внешних воздействий и изменять её постепенно (т.е. с конечным ускорением) под действием силы.

Импульсом тела (материальной точки) называется векторная физическая величина, равная произведению массы тела на его скорость: .

Импульс системы материальных точек равен векторной сумме импульсов точек, составляющих систему: .

Второй закон Ньютона: скорость изменения импульса тела равна действующей на него силе:

.

Если масса тела остается постоянной, то ускорение, приобретаемое телом относительно инер­ци­аль­ной системы отсчета, прямо пропорционально действующей на него силе и обратно пропорционально массе тела:

.

Третий закон Ньютона: силы, с которыми действуют друг на друга взаимо­дей­ствующие тела, равны по величине и противоположны по направлению:

,

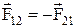где – сила, действующая на первое тело со стороны второго,

– сила, действующая на второе тело со стороны первого.

Из третьего закона следует, что в любой механической системе материальных то­чек геометрическая сумма всех внутренних сил (т.е. сил, с которыми взаимо­действуют между собой материальные точки системы) равна нулю.

2.2. Динамика вращательного движения твердого тела

Вращательное действие силы харак­те­ризуется мо­ментом силы относительно точки (рис. 5а) и относительно оси (рис. 5б).

Для того чтобы определить момент силы относительно точки О, проведем из точки О радиус-вектор в точку приложения силы (рис. 5а). Моментом силы относительно точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора на силу :

Модуль момента силы M = r×F×sina = F×d, где d = r×sina – плечо силы.

Для того чтобы определить момент силы относительно оси Z, выберем на оси Z произвольную точку, найдем момент силы относительно этой точки, а затем спроецируем на ось Z момент силы относительно точки. Таким образом, момент силы относительно оси – величина скалярная.

Разложим силу на три составляющие (рис. 5б):

– осевая, параллельная оси вращения,

– радиальная, перпендикулярная оси вращения,

– касательная, перпендикулярная и оси вращения.

Составляющую можно определить как проекцию силы на направление вектора , направленного по касательной к окружности радиусом R, проведенной через точку приложения силы перпендикулярно оси вращения. Направление вектора образует с осью Z правовинтовую систему.

Составляющие и вращения тела относительно оси Z не вызывают. Вращающее действие силы обусловлено составляющей . Можно показать, что момент силы относительно оси Z

Рис. 5

Инертные свойства тела при вращательном движении характеризует м омент инерции. Он зависит от распределения массы тела относительно оси вращения. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси: .

– момент инерции системы материальных точек;

– момент инерции тела, где – плотность тела.

Рис. 6

Момент инерции тела относительно произвольной оси может быть рассчитан по теореме Штейнера: момент инерции тела относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр инерции и параллельной O'O, и произведения массы тела на квадрат расстояния между осями (рис. 6): .

Моментом импульса материальной точки относительно некоторой точки называется векторная величина, равная векторному произведению радиуса-вектора на импульс материальной точки (рис. 7а):

.

Моментом импульса системы материальных точек называется геометрическая сумма моментов импульсов точек, составляющих систему:

.

Моментом импульса материальной точки относительно оси Z называется скалярная величина, равная проекции момента импульса относительно произвольной точки, лежащей на оси Z, на эту ось. Аналогично моменту силы относительно оси, момент импульса относительно оси Z

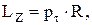
где p_t – проекция импульса на направление вектора , направленного по касательной к окружности радиусом, проведенной через материальную точку перпендикулярно оси вращения (рис. 7б). Направление вектора образует с осью Z правовинтовую систему.

Рис. 7

Момент импульса тела относительно оси вращения

L_Z = I_Z×w_Z,

где I_Z – момент инерции тела относительно оси Z, w_Z – проекция угловой скорости тела на ось Z. Для однородного тела, вращающегося относительно оси симметрии:

.

Основной закон динамики вращательного движения:

Скорость изменения момента импульса тела относительно оси равна результирующему моменту внеш­них сил относительно этой же оси (проекция углового ускорения на ось пропор­циональна результирующему моменту внешних сил относительно оси и обратно пропорциональна моменту инерции тела относительно этой же оси):

Из законов динамики поступательного и вращательного движений следует условие равновесия тел:

Поиск по сайту: