Работа и механическая энергия

3.1. Работа и мощность при поступательном и вращательном движениях

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.

Элементарной работой силы называется величина, равная скалярному произведению силы на элементарное перемещение :

,

где – элементарный путь точки приложения силы за время dt, a – угол между векторами и .

Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:

.

Если = const, то А= × .

При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:

,

если М_w = const, то А = М_w×j.

Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:

– средняя мощность; – мгновенная мощность.

При вращательном движении мощность определяется следующим образом:

.

3.2. Консервативные и неконсервативные силы

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

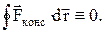
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

3.3. Кинетическая энергия при поступательном и вращательном движениях

Кинетической энергией тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).

Кинетическая энергия поступательного движения . Кинетическая энергия вращательного движения .

При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:

.

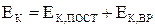Свойства кинетической энергии.

1. Кинетическая энергия является конечной, однозначной, непрерывной функ­цией механического состояния системы.

2. Кинетическая энергия не отрицательна: Е_К³ 0.

3. Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.

4. Приращение кинетической энергии тела равно работе всех сил, действу­ю­щих на тело: .

3.4. Потенциальная энергия

Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.

Е_П1 - Е_П2 = -DЕ_П = А_12конс, .

Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.

.

Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.

Свойства потенциальной энергии.

1. Потенциальная энергия является конечной, однозначной, непрерывной

функ­цией механического состояния системы.

2. Численное значение потенциальной энергии зависит от выбора уровня с

нулевой потенциальной энергией.

Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:

,

причем , , .

Примеры потенциальной энергии:

1) – потенциальная энергия тела массой m, поднятого на высоту h относительно нулевого уровня энергии в поле силы тяжести;

2) – потенциальная энергия упругого деформированного тела, Dх – деформация тела.

Поиск по сайту: