 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 5
Вагон массой 20 т, движущийся равнозамедленно, под действием силы трения в 6 кН через некоторое время останавливается. Начальная скорость вагона равна 54 км/ч. Найти работу сил трения и расстояние, которое вагон пройдет до остановки.
Дано:
| m = 20 × 10 3 кг Fтр = 6 × 10 3 Н u = 15 м/c | Решение
По закону сохранения механической энергии изменение полной механической энергии определяется работой неконсервативных сил, то есть
 .
|
| AТР -? Dr -? | Так как механическая энергия вагона равна его кинетической энергии, в качестве неконсервативной силы выступает сила |
трения. Так как в конце пути скорость вагона равна нулю, то
.
Итак: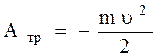 
=-2250 кДж.
По определению, для работы, совершаемой постоянной силой трения:
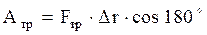
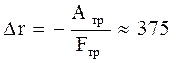м.
Ответ: r = 375 м.
Задача 6 После упругого удара нейтрона о ядро атома углерода он движется в направлении, перпендикулярном начальному. Считая, что масса М ядра углерода в n=12 раз больше массы m нейтрона, определить, во сколько раз уменьшается энергия нейтрона в результате удара.
Дано:
| Решение Ведем обозначения: u1 – скорость нейтрона до удара, u1¢ – после удара; u2 – скорость ядра углерода после удара (до удара она равна нулю). |
| a -? |
По законам сохранения импульса и энергии соответственно имеем:
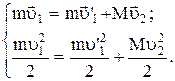
По условию задачи требуется найти отношение
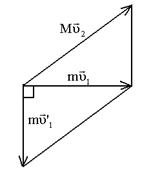
Из треугольника импульсов (смотри рисунок)
имеем: (mu1)2+(mu¢1)2=(Mu2)2.
С учетом записанных выражений, а также соотношения n=M/m получим
u12-u¢12=nu22;
u12+u¢12=n2u22.
Разделив почленно последние равенства, получаем
.
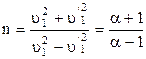Отсюда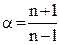 
=1,18.
Ответ: a = 1,18.
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м2, вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
Дано:
| R = 1м J = 130 кг × м2 n1 = 1c-1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме: |
| n2 -? |
L1 = L2, (1)
где L1 - импульс системы «платформа + человек на краю платформы», L2 - импульс системы «платформа + человек в центре платформы».
L1 = J1w1 = (J+mR2)×2pn1, (2)
L2 = J2w2 = J×2pn2, (3)
где mR2 - момент инерции человека, J1 = J+mR2 - момент инерции системы «платформа + человек на краю платформы», J2 - момент инерции системы «платформа + человек в центре платформы», w1 и w2 - соответствующие угловые скорости системы. Решая систему уравнений (1) - (3), получаем
n2 = n1(J+mR2)/J = 1,5 об/с.
Ответ: n2 = 1,5 с-1.
Поиск по сайту: