АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение временной функции переходного процесса и критерия устойчивости САР по характеристическому уравнению

Читайте также:
  1. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  2. I. Психологические операции в современной войне.
  3. I.1. Римское право в современной правовой культуре
  4. II звено эпидемического процесса – механизм передачи возбудителей.
  5. II. Основные задачи и функции
  6. II. Показатели финансовой устойчивости предприятия.
  7. II. Принципы процесса
  8. III. Предмет, метод и функции философии.
  9. VI. Педагогические технологии на основе эффективности управления и организации учебного процесса
  10. VII. По степени завершенности процесса воздействия на объекты защиты
  11. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  12. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ

 

Устойчивость системы определяется по положению характеристических корней р] и р2 на координатной плоскости (в координатах мнимых Im и действительных Rе чисел). Для определения корней характеристического уравнения приравняем к нулю знаменатель

 

Решение уравнения

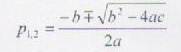
Найдем дискриминант уравнения

 

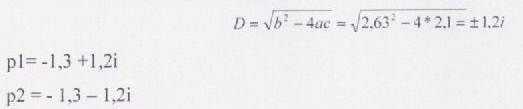
По критерию Ляпунова, если два положения корней находятся в отрицательной плоскости относительно оси Im, то система устойчива, чем дальше положение корней от оси Im, тем более устойчива система

 

 

 

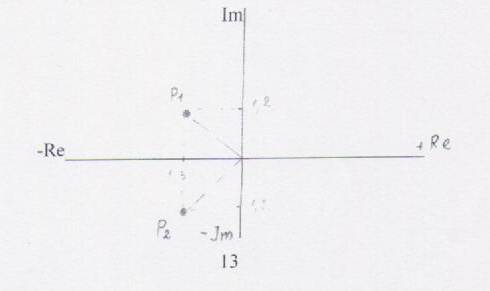
Это показывает, что под влиянием изменения на входе, в системе возникает регулирующее воздействие, при котором система стремится к своему первоначальному состоянию.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)