Расчет надежности резьбовых соединений

Вероятность безотказной работы резьбового соединения рассчитывается как произведение вероятностей безотказной работы по четырем основным критериям:

P_рез=P₁·P₂·P₃·P₄,

где P₁ – вероятность безотказнойработы по нераскрытию стыка;

P₂ – вероятность безотказной работы по несдвигаемости деталей стыка;

P₃ – вероятность безотказной работы по статической прочности;

P₄ – вероятность безотказной работы по сопротивлению усталости.

Полагаем, что распределение вероятностей безотказной работы соединения по всем критериям подчиняется закону нормального распределения. Тогда P₁, P₂, P₃, P₄ определяются в зависимости от значения соответствующей квантили u_p1, u_p2, u_p3, u_p4 с учетом соответствующих коэффициентов запаса n₁, n₂, n₃, n₄.

; ,

где , - средние значения затяжки и растягивающей силы;

, - коэффициенты вариации соответственно и .

=

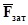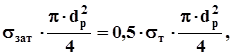
где - напряжение от силы затяжки;

- предел текучести материала болта;

d_p – расчетный диаметр резьбы;

- коэффициент, учитывающий ослабление затяжки из-за

обмятия стыка, =1,1;

- коэффициент внешней основной нагрузки на стык.

Зависит от податливости детали и болта. =0,2-0,3.

Значение принимается в зависимости от метода контроля затяжки резьбового соединения:

Способ контроля	Динамометрическим ключом	По углу поворота гайки	По удлинению болта
	0,09	0,05	0,02

Значение коэффициента вариации растягивающей силы:

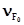=0,1

u_p2=-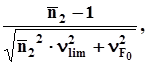

где - среднее значение коэффициента трения;

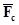- среднее значение сдвигающей силы,

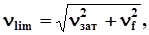
где - коэффициент вариации коэффициента трения определяется,

считая, что среднее квадратичное отклонение равно 1/6 части допуска.

u_p3=-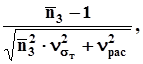

где k – коэффициент, учитывающий деформацию кручения болта

(k=1,3).

В технических расчетах принимаем .

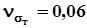u_p4=- ,

где - предел выносливости болта;

- действующие напряжения, приведенные к симметричном

циклу.

,

где - среднее значение предела выносливости гладкого образца;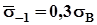

- коэффициент влияния абсолютных размеров ( =1);

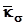- среднее значение эффективного коэффициента концентрации напряжения, зависит от предела прочности материала

(Мпа)
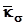
	3,0	3,9	4,8	5,2

Значение может быть вычислено: ,

где g – коэффициент чувствительности материала к концентрации

напряжений.

Для углеродистых сталей g=0,5-0,6.

Для легированных сталей g=0,7-0,8.

- среднее значение теоретического коэффициента концентрации напряжений. Зависит от шага резьбы и радиуса ее впадины.

,

где Р – шаг резьбы;

R– радиус впадины резьбы. Рассеяние радиуса впадины не зависит от точности резьбы и составляет (0,1-0,144)Р;

‑ коэффициент. Для стандартных болтов и гаек =1; для соединений типа стяжек =1,5-1,6.

‑ коэффициент технологического упрочнения.

Для нарезанной резьбы =1; для накатанной резьбы =1,2-1,3.

,

где - среднее значение максимальной нагрузки цикла;

0,5 - среднее значение амплитуды нагрузки. ;

- коэффициент чувствительности материала к асимметрии цикла

( =0,1);

- коэффициент вариации напряжения ;

- коэффициент вариации 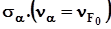предела выносливости;

,

- коэффициент вариации предела выносливости детали одной

плавки, =0,06-0,08;

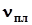- коэффициент вариации среднего предела выносливости по

плавкам, 0,08;

- коэффициент вариации эффективного коэффициента

концентрации напряжений;

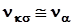- коэффициент вариации концентрации напряжений

.

Поиск по сайту: