ЧАСТЬ 1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Маховик в виде колеса массой m = 30 кг и диаметром 60 см вращается с угловой скоростью w, изменяющейся по закону w = Аt¹⁰, где А = 2 рад/с¹¹. Найти закон движения j(t), угловое ускорение e (t), момент сил М(t) и момент количества движения L(t). Вычислить эти величины через 2 с после начала движения. Считать начальный угол j(t =0) = j₀ = 0.

Решение.

Перевод в СИ

m = 30 кг 30 кг

D = 60 см 0,6 м

w = Аt¹⁰ = 2× t¹⁰рад/с¹¹ 2× t¹⁰рад/с

t = 2 c 2 c

Определить: j(t), e (t), М(t), L(t).

Если известен закон движения, то угловая скорость определяется как первая производная от j(t) по времени:

dj

w(t) = ¾¾ (1)

dt

Закон движения j(t) находится решением обратной задачи, т.е. интегрированием угловой скорости по времени:

j(t) = w(t) d t + j_{0 (2)}

При w(t) = 2 ×t¹⁰ ,с учетом j₀ = 0:

j(t) = 2×t¹⁰ d t + j₀ = (3)

В момент времени t = 2 с маховик повернулся на угол j(t =2 с) = = 372,3» 372 рад.

Угловое ускорение определяется как первая производная от угловой скорости по времени:

dw d

e = ¾¾ = ¾¾ (2 ×t¹⁰) = 10 × 2× t⁹ (4)

dt dt

В момент времени t = 2 c угловое ускорение равно:

e (t = 2c) = 10 × 2 × 2⁹ = 10240» 1,02× 10⁴ рад/с²

Момент сил можно определить из основного закона динамики для вращательного движения твердого тела:

М = I × e (5)

где I - момент инерции тела.

В нашем случае момент инерции колеса равен:

I = mR² = mD²/4 (6)

Подставляя выражения (4) и (6) в (5) получим:

mD² 20 t⁹

М = ¾¾ ×¾¾

При t = 2 c

30 × (0,6)² 20×2⁹

M = ¾¾ ¾¾ ¾¾ ¾¾ = 27648» 2,77 × 10⁴ Н×м

Момент количества движения равен:

L = I w (7)

Подставляя выражения для w и (6) в (7) получим:

mD² 2 t¹⁰

L = ¾¾ ¾¾

При t = 2 c

30× (0,6)² × 2× 2¹⁰

L = ¾¾ ¾¾ ¾¾ = 5529,6 = 5,53× 10³ кг м²/с

Проверим размерность полученных выражений.

рад с¹¹

[j] = [А] [t¹¹] = ¾¾¾¾ = рад;

с¹¹

рад с⁹

[e] = [А] [t⁹] = ¾¾¾¾ = рад/с²

с¹¹

mD² × A t⁹ кг м² с⁹ кг м м

[M] = [¾¾¾¾¾¾¾¾ ] = ¾¾¾¾ = ¾¾¾¾ = Н м

4 11 с¹¹ с²

кг м² c¹⁰

[L] = [ m D² A t¹⁰ ] = ¾¾¾¾ = кг м² с^-1

c¹¹

Ответ: j(t=2) =372рад, e(t=2с)= 1,02× 10⁴ рад/с², М(t) =2,77 × 10⁴ Н м

L(t) = 5,53× 10³ кг м²/с

Пример 2. Соковыжималка раскручивается до 7200 об/мин. Определить силу, действующую на кусочек яблока массой 5г, при диаметре камеры D = 24 см. Вычислить линейную скорость кусочка яблока. Оценить мощность соковыжималки, если максимальные обороты достигаются за 8с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 100 г. Яблочная масса при загрузке составляет 300 г.

Решение. СИ

n = 7200 об/мин = 120 с^-1

R = D/2 = 12 см = 0,12 м

m = 5 г = 5 ·10^{-3 кг}

m₁ = 100 г = 0,1 кг

m₂ = 300 г = 0,3 кг

t = 8с

Определить: силу F, скорость V, мощность Р

Кусок яблока движется по круговой траектории с центростремительным ускорением

а = V²/ R. (1)

Сила, действующую на кусочек яблока со стороны барабана, равна

F= mV²/ R.

С силой F кусок яблока прижимается к барабану. Поэтому искомая сила равна

F= mV²/ R = F= mw² R, (2)

где V = w R –линейная скорость кусочка яблока;

w = 2π n - угловая скорость

Проверим размерность подставляя:

кг· с^-2 · м

[F] = [¾¾¾¾¾] = кг· м·с^-2 = Н

Проведем вычисления:

Сила F = mw² R= 5 ·10^-3 ·(2 ·3,14)² ·(120)²×0,12=5·10^-3 ·4·9,86·1,44·10⁴ ×0,12=2,84·10³ Н

Линейная скорость кусочка яблока:

V = w R = 2π n R =2·3,14 ·120 · 0,12 =30.432 ≈ 30.4 м/с

Мощность соковыжималки можно оценить, вычислив кинетическую энергию вращающегося барабана вместе с содержимым и разделив её на время раскручивания.

Кинетическая энергия вращения равна:

Е_кин = (I + I₁) w² /2

где I = m₂ R ² – момент инерции яблочной массы;

I₁ = m₁ R ² / 2 + m₁ R ² момент инерции полуцилиндра, состоящего из диска и кольца.

I = 0,3· (0,25)² = 0.0185 =1.875·10^-2 кг·м² ≈ 1.88·10^-2 кг·м²

I₁ =(0.05 +0.1) · (0,25)² = 0.93675·10^-2 кг·м²≈ 0.937·10^-2 кг·м²

Е_кин= (1.88 + 0.937) ·10^-2 ·(2π 120)² / 2 = 2.82 ·10^-2 · 2· (3,14)² 1.44· 10⁴ ≈ 8.01·10³ Дж.

Мощность соковыжималки:

Р = Е_кин / t =8.01·10³ / 8 ≈ 10³ Вт

Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2.

Ответ: сила, прижимающая кусочек яблока к барабану F = 2,84·10³ Н,

линейная скорость кусочка яблока:V ≈ 30.4 м/с; мощность соковыжималки Р ≈ 10³ Вт.

Пример 3. Автомобиль тянет платформу с грузом, представляющим собой прямоугольную форму весом 250 кг. Коэффициент трения между платформой и грузом 0,05, вес платформы 820 кг. Сила с которой тянет автомобиль платформу изменяется по закону F=Аt, где А=4,25[кг×м/с³] – некоторая постоянная. Определить: 1) момент времени t₀, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а₁ и платформы а₂ в процессе движения.

Решение.

m₁=250 кг Описанный процесс схематично изображен на рис.1.

m₂=820 кг Сила, с которой машина тянет платформу, можно выразить

f=0,05 формулой F=F_тр+m₂a₂ (1), где F_тр= m₁a₁ (2). Максимальное F=4,25t значение силы трения равно F_тр.max= f m₁ g (3),

______________

Найти

t₀=? где g=9,81 м/с² - есть ускорение свободного падения.

а₁=? Используя выражения (1), (2) и (3), определим ускорение а₂ и,

а₂=? подставим его в очевидное неравенство, а₂ ³ а₁, показывающее

Рис. 1.

предельное значение ускорения, при котором груз уже скользит по платформе.

а₂ = 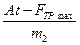; а₁=fg; тогда .

Во время t=t₀ , из чего выразим t₀= .

Во время t£t₀ а₁=а₂=

Во время t£t₀ а₁=fg=const, а₂= .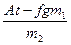

Так как исходные данные приведены в системе единиц СИ, то подставим в полученные выражения числовые значения и рассчитаем требуемые неизвестные.

t₀=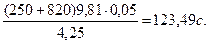

а₁=9,81×0,05=0,49 м/с².

а₂= .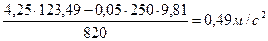

Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2.

Ответ: 1) время, после начала движения при котором платформа начнет выскальзывать из под груза больше t₀= 123,49 с; 2) ускорение груза достигнет а₁= 0,49 м/с²; 3) платформа должна двигаться с ускорением больше, чем а₂= 0,49 м/с².

Пример 4. С башни, высотой 20 м, горизонтально со скоростью 10 м/с из пращи брошен камень массой 400 г. Пренебрегая сопротивлением воздуха определить для момента времени 1с после начала движения кинетическую и потенциальную энергии.

Решение.

H= 20 м Запишем формулы для расчета кинетической и потенциа-

u₀= 10 м/с льной энергий:

m= 400 г = 0,4 кг Т = ; П = m×g×h.

t= 1 с

______________

Найти: В формулах не все данные известны. Необходимо найти

Т =?; П =?. общую скорость движения камня через 1 с и высоту на

которой камень будет находиться через это время. Скорость движения при снижении камня по вертикали определяется выражением u_y = g×t, а полная скорость движения u² = u₀² + u_y², где u₀ = const – постоянная скорость движения камня по горизонтали, u_y – скорость равнопеременного движения камня по вертикали. Подставив полученные формулы в выражение для кинетической энергии, окончательно получим:

Т = m ×(u₀²+g² × t²) / 2.

За время t камень опустится на высоту h₁ = , тогда потенциальная энергия камня будет равна

П = m×g×(H - ).

Проведем вычисления: Т = m ×(u₀²+g² × t²) / 2 = 0,4×(10² + 9,81²×1²) / 2 = 39,2 Дж;

П = m×g×(H - ) = 0,4×9,81× (20 – 9,81×1²/2) = 59,2 Дж.

Ответ: 1) кинетическая энергия камня через секунду после начала движения равна Т = 39,2 Дж; 2) потенциальная энергия равна П = 59,2 Дж.

Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2.

Пример 5. В цилиндре под поршнем находится водород массой 20 г, при температуре 25⁰С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического процесса расширения и работу, совершенную газом. Изобразить процесс графически.

Решение. СИ

М = 20г 0.02 кг

T₁ = 25⁰C Т₁ = 298 К

V_1а/ V_2а = 5

V_2и/ V_1и = 1/5

R = 8,31 Дж/моль∙град

µ=2 ∙10^-3 кг/моль

i = 5

γ = 1,4

________________________________

Определить: Т₂=?; А₁=?; А₂=?.

Отношение температур и объемов газа, совершающего адиабатический процесс, описываются равенством:

,

где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме. Отсюда получаем выражение для конечной температуры Т₂:

.

Подставляя численные значения, получаем:

Т₂ = 298∙(1/5)^1,4-1 = 298∙0.525 = 156,5 К.

Работа газа при адиабатическом расширении определим по формуле:

Подставляя цифровые значения в полученное выражение, получаем:

.

Работа газа при изотермическом процессе может быть выражена формулой:

.

Подставляя известные числовые значения, величин входящих в формулу, и выполняя арифметические операции, находим работу при изотермическом процессе:

.

Знак «минус» показывает, что при сжатии газа работа совершается над газом внешними силами.

График описанного процесса представлен на рис.1.

Рис. 1.

Ответ: Температура в конце адиабатического процесса расширения Т₂ = 156,5 К.

Работа, совершенная газом для точек 2,3 равна А₁=8,62∙10⁴Дж, А₂=-2,08∙10⁴Дж.

Пример 6. Определить плотность смеси газов (60 % пропана - С₃Н₈,30%, бутана - С₄ Н₁₀ и 10% метана - CH₄) находящихся в баллоне при температуре 27 ⁰С и давлении 0.11МПа.

Решение. СИ

m₁(С₃Н₈) = (3×12 +8×1) × 10^-3 = 44×10^-3кг/моль

m₁/m= 0.6 - “ -

m₂ (С₄H₁₀) = (4×12 + 10×1) ×10^-3=56×10^-3 кг/моль

m₂/m =0.3 - “ -

m₃ (СН₄) = (12 + 4×1) ×10^-3 = 16×10^-3 кг/моль

m₃/m = 0.1 - “ -

t = 27⁰C Т = 300 К

P = 0.11 MПа 0.11× 10⁶ Па

____________________________________

Определить: r =?

По закону Дальтона давление смеси газов P равно сумме парциальных давлений газов, составляющих смесь P₁(C₃ H₈), P₂(C₄ H₁₀),P₃ (CH₄):

P = P₁ + P₂ + P₃ (1)

Для каждого газа справедливо уравнение состояния (Клапейрона -Менделеева):

P_i V = (m_i /m_i)RT (2)

Из выражения (2) можно выразить парциальное давление:

P_i = (m_i /m_i)RT/V (3)

Уравнение Клапейрона - Менделеева справедливо и для смеси газов:

P V = (m /m)RT (4)

Плотность газа равна:

r = m/V = Pm/ RT (5)

Молярную массу смеси можно найти подставив (3) в (1):

P = (m₁/m₁)RT/V + (m₂ /m₂)RT/V + (m₃ /m₃)RT/V = (m/m) RT/V (6)

Из уравнения (6) молярная масса m равна:

m = (m₁/m₁m + m₂/m₂m + m₃/m₃m)^-1 (7)

Подставляя (7) в (5) получим выражение для плотности смеси:

r = P/ RT (m₁/m₁m + m₂/m₂m + m₃/m₃m)

Проверим размерность получившейся формулы:

[r]=[P] /[R][T] [m^-1]=Па/ (Дж моль^-1К^-1) К (кг/моль)^-1=Па/Дж кг^-1=Нм^-2 кг/Нм= кг/м³

r = 0.11×10⁶ /8.31 300 (0.6/44×10^-3 + 0.3/ 56×10^-3 + 0.11/6×10^-3) = (0.11× 39.6 /8.31×3×) × 10^6-2-3 = 0.175×10 =1.75 кг/м³

Ответ: плотность смеси газов r = 1.75 кг/м³.

Поиск по сайту: