 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частичные автоматы
|
Читайте также: |
В инженерной практике часто встречаются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются. Такие последовательности будем называть запрещенными входными словами данного автомата, а сам автомат – частичным автоматом. У частичного автомата функции переходов и выходов определены не на всех парах ai, xj. На месте неопределенных состояний и выходных сигналов ставится прочерк. При синтезе обычно производят доопределение частичного автомата, чтобы его схемная реализация получилась как можно проще.
Пример таблицы переходов и выходов частичного автомата Мили:
| xj/ ai | a0 | a1 | a2 | a3 |
| x1 | a1 / y1 | a2 / y2 | a3 / y3 | a2 / y1 |
| x2 | - / - | - / - | a0 / y4 | a0 / y2 |
Контрольные вопросы к лекции 4:
1.Какие схемы используются в ЦА?
2.Дайте определение автомата?
3.Что такое «конечный» автомат?
4.Что подразумевается под термином «состояние»?
5.Дайте определения понятиям «алфавит», «слово», «буква»?
6.Что такое «пустое слово» и «пустая буква»?
7.Дайте определение понятию «такт»?
8.Какие, кроме детерминированных, существуют автоматы?
ЛЕКЦИЯ 5
Элементарные автоматы
Структурным синтезом занимается структурная теория автоматов. Основная цель этой теории – нахождение общих приемов построения сложных структурных схем автоматов из более простых автоматов, называемых элементарными автоматами. На практике в большинстве случаев применяют элементарные автоматы с двумя внутренними состояниями. В процессе синтеза элементарные автоматы соединяют между собой с помощью логических элементов.
Первая задача, решаемая при структурном синтезе, заключается в выборе системы элементов, из которых должны строиться заданные автоматы. Для того чтобы можно было построить схему любого конечного автомата, эта система элементов должна быть структурно полной.
Теорема о структурной полноте формулируется следующим образом:
- Для того чтобы система элементов была структурно полной, необходимо и достаточно, чтобы она содержала какую-либо функционально полную систему логических элементов и хотя бы один элементарный автомат с двумя устойчивыми состояниями, обладающий полной системой переходов и выходов.
Полнота переходов в автомате означает, что для любой пары состояний ai и aj существует хотя бы один входной сигнал, который переводит автомат из состояния ai в состояние aj, причем i = j и  , т.е. в каждом столбце таблицы переходов должны встречаться все состояния. Полнота выходов автомата означает, что в каждом состоянии автомат выдает выходной сигнал, отличный от сигналов, выдаваемых в других состояниях.
, т.е. в каждом столбце таблицы переходов должны встречаться все состояния. Полнота выходов автомата означает, что в каждом состоянии автомат выдает выходной сигнал, отличный от сигналов, выдаваемых в других состояниях.
Требование полноты системы выходов связано с необходимостью различать внутренние состояния элементарных автоматов, так как в автомате, не обладающем полной системой выходов, различить состояния невозможно и, следовательно, невозможно обеспечить заданные условия функционирования схемы, построенной на его основе.
Если элементарный автомат не имеет полной системы переходов, то это значит, что отсутствует переход хотя бы одного вида. Поэтому построить на основе такого элементарного автомата схему, в которой бы осуществлялись все возможные переходы из одного состояния в другое, нельзя. Таким образом, для построения любого конечного автомата необходимо иметь элементарные автоматы, обладающие полной системой, как переходов, так и выходов. Рассмотрим конкретные типы элементарных автоматов, имеющих полную систему переходов и выходов и нашедших применение в вычислительной технике.
В настоящее время в вычислительной технике, как правило, используются элементарные автоматы, имеющие следующие особенности:
1. Элементарные автоматы являются автоматами Мура с двумя внутренними состояниями.
2. Автомат выдает два различных выходных сигнала, соответствующих двум его внутренним состояниям. В дальнейшем состояния автомата и его выходные сигналы будем обозначать одной буквой Q и кодировать цифрами 0 и 1.
3. Элементарные автоматы могут иметь в общем случае несколько физических входов.
В качестве элементарных автоматов в вычислительной технике используются триггеры различных типов (рис. 5.1). Рассмотрим некоторые из них.

Рис. 5.1
Т-триггер.
Т- триггером называют автомат Мура с двумя устойчивыми состояниями и одним входом Т, который изменяет свое состояние на противоположное всякий раз, когда на вход Т поступает единичный сигнал.
Таблица переходов Т-триггера:
| yg | ||
| xj /ai | ||
| T = 0 | ||
| T = 1 |
Из таблицы переходов видно, что Т-триггер обладает полной системой переходов и выходов, поскольку для каждой пары состояний (0-0, 0-1, 1-0,1-1) имеется входной сигнал, обеспечивающий переход из одного состояния в другое.
Кроме того, каждое состояние автомата отмечено отличным от других выходным сигналом. На практике более удобно вместо отмеченных таблиц переходов пользоваться так называемыми матрицами переходов элементарных автоматов.
Матрица переходов
| T | Q(t) | Q(t+1) |
Она определяет значения сигналов на входах элементарного автомата, обеспечивающих каждый их четырех возможных переходов. Здесь Q(t) и Q(t + 1) – состояния автомата в моменты времени t и t + 1 соответственно.
Поскольку Т-триггер имеет один вход, а число возможных переходов равно четырем, то матрица переходов имеет четыре строки.
Для записи закона функционирования Т-триггера в аналитическом виде составим диаграмму Вейча:
| T\Q(t) | ||
Из диаграммы имеем:  .
.
Поскольку эта формула совпадает с аналитической записью ПФ логической неравнозначности (сложение по модулю два), то Т-триггер часто называют триггером со счетным входом, а входной сигнал, поступающий на вход Т, счетным сигналом.
На практике кроме асинхронного Т-триггера, работу которого мы рассмотрели, используют так же и синхронный Т-триггер, который меняет свои состояния только при Т = 1 и С = 1. Если хотя бы один из этих сигналов равен нулю, то триггер сохраняет свое состояние. Вход С называют входом синхронизации.
Поясняющая работу комбинационная схема и обозначение синхронного
Т-триггера представлены на рис. 5.2:
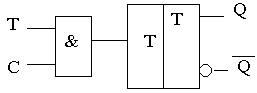

Рис.5.2.
D-триггер.
D-триггером (триггером задержки) называют элементарный автомат Мура с двумя устойчивыми состояниями и одним входом D таким, что Q(t + 1) = D(t). Название D-триггера происходит от английского слова “delay” – задержка. Из определения следует, что состояние триггера в момент времени t + 1 повторяет значение входного сигнала D(t) в момент времени t (отсюда и название триггера задержки).
Матрица переходов D-триггера:
| D | Q(t) | Q(t + 1) |
Обозначение синхронного D-триггера:

Рис. 5.3
В синхронном D-триггере при С = 0 триггер свое состояние не меняет, а при С=1 работает так же, как и асинхронный, то есть  .
.
Граф D-триггера (рис. 5.4):

Рис. 5.4
RS-триггер.
RS- триггером называют автомат Мура с двумя устойчивыми состояниями, имеющий два входа R и S. При S = 1 триггер устанавливается в состояние 1, а при R = 1 – в состояние 0. Одновременная подача двух сигналов, равных 1, запрещена, т.е. R S = 0. В соответствии с состоянием, принимаемым триггером, вход S называет единичным входом, а вход R – нулевым.
Матрица переходов RS-триггера:
| R | S | Q(t) | Q(t+1) |
| b1 | |||
| b2 |
Переход триггера из 0 в 0 возможен при двух комбинациях входных сигналов: R = 0, S = 0 и R = 1, S = 0. Поэтому в первой строке матрицы переходов в столбце R поставлен неопределенный коэффициент b1 = 0 v 1. Аналогично переход из состояния 1 в 1 также возможен при двух комбинациях входных сигналов: R = 0, S = 0 и R = 0, S = 1. Поскольку при таком переходе значения сигнала на входе S безразлично, то в нижней строке матрицы переходов в столбце S записан коэффициент b2. По матрице переходов можно построить граф RS-триггера.
Автоматы, которые могут переходить из одного состояния в другое под действием нескольких комбинаций входных сигналов, называются автоматами с избыточной системой переходов. Избыточность можно использовать в процессе синтеза для упрощения схемы, придавая коэффициентам b1 и b2 такие значения, которые позволяют минимизировать число элементов. Поэтому, если схемы двух элементарных автоматов равноценны по сложности, то предпочтение отдают автомату, имеющему большую избыточность системы переходов.
Запишем закон функционирования RS-триггера в аналитическом виде, для чего составим по матрице переходов диаграмму Вейча:
| SQ(t) | ||||
| R | ||||
| - | - |
Запрещенные комбинации входных сигналов при минимизации заполним единичными значениями.
Тогда имеем: 
Поиск по сайту: