ЛЕКЦИЯ 3

Основные понятия и определения

Преобразование функции в минимальную конъюнктивную нормальную форму (КНФ)

Для того, чтобы получить выражение заданной ПФ в форме, содержащей минимальное количество букв, следует, кроме минимальной ДНФ, получить также минимальную КНФ, и выбрать ту из них, которая содержит меньшее число букв. Существуют различные методы минимизации КНФ. Рассмотрим один из таких методов, основанный на минимизации функции 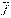и в переходе с помощью формулы де Моргана к функции f. При минимизации 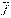можно использовать все методы, которые применялись ранее при нахождении минимальной ДНФ. После получения минимальной ДНФ функции

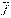с помощью формул де Моргана переходят к минимальной КНФ функции f.

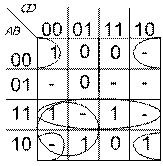
Пример 3.1. Найти минимальную КНФ функции . Диаграмма Вейча имеет вид:

Из диаграммы получим: .

Тогда: 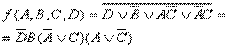– минимальная КНФ.

Минимизация не полностью определенных переключательных функций

В ЭВМ иногда применяются КС, закон функционирования которых определен не полностью. В таких схемах некоторые комбинации сигналов на входы никогда не подаются. Эти комбинации входных сигналов называются запрещенными. Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения 0 или 1. Поэтому при синтезе КС с не полностью заданным законом функционирования можно произвольно задать значение выходных сигналов для запрещенной комбинации входных сигналов, поскольку нормальная работа схемы при этом не нарушается. Обычно выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему. Работа схем с запрещенными комбинациями входных сигналов описывается не полностью определенными ПФ, т.е. функциями, значения которых определены не на всех наборах аргументов. Поэтому минимизация не полностью определенных ПФ с помощью карт Карно сводится к такому доопределению ПФ, при котором получаются группы с максимальным числом соседних единиц в каждой группе, а число таких групп минимально. При этом ПФ будет содержать минимум букв.

Пример 3.2. Найти минимальную ДНФ и минимальную КНФ не полностью определенной ПФ: , . На остальных наборах функция не определена.

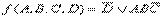–– минимальная ДНФ,

;

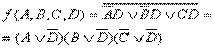– минимальная КНФ.

Минимизация систем переключательных функций

Работа КС, имеющей n входов и m выходов, описывается системой m переключательных функций, каждая из которых определяет закон функционирования схемы по одному выходу (рис. 3.1).

Если провести минимизацию ПФ, входящих в систему независимо друг от друга, то получится схема, содержащая m изолированных цепей, в общем случае не минимальная. Однако эту схему можно существенно упростить за счет объединения участков схемы, реализующих одинаковые члены.

Рис.3.1. Комбинационная схема

Общая идея минимизации схем со многими выходами сводится к получению выражений для системы ПФ, в которых наилучшим образом используются конъюнкции, общие для нескольких функций. Покажем, как производится минимизация системы ПФ.

Пример 3.3. Пусть дана система из трех ПФ от 4-х аргументов:

Схема, реализующая систему ПФ, приведена на рис. 3.2.

Рис. 3.2

Вопросы к лекции 3:

1. В какой форме должна быть представлена булева функция и как её надо преобразовать для реализации на логических элементах булева базиса И, ИЛИ, НЕ?

2. В чём заключается тривиальный способ реализации булевой функции на MS?

3. За счёт чего можно реализовать булеву функцию (n + 1)-го аргумента на MS, имеющих число управляющих входов n?

4. В какой форме должна быть представлена булева функция и как её надо преобразовать для реализации на логических элементах универсального базиса И-НЕ?

5. В какой форме должна быть представлена булева функция и как её надо преобразовать для реализации на логических элементах универсального базиса ИЛИ-НЕ?

6. Какие ПФ называются не полностью определенными?

7. Как происходит минимизация не полностью определенных переключательных функций?

8. В чем общая идея минимизации схем со многими выходами?

Поиск по сайту: