Структурная схема конечного автомата

В структурной теории автомат представляют в виде композиции двух частей: запоминающей части, состоящей из элементов памяти, и комбинационной части, состоящей из логических элементов (рис. 6.1):

Рис. 6.1

Комбинационная схема строится на логических элементах, образующих функционально полную систему, а память – на элементарных автоматах, обладающих полной системой переходов и выходов.

Каждое состояние абстрактного автомата a_i, где i = {0, М}, кодируется в структурных автоматах набором состояний элементов памяти Qr, r = {1, R}. Поскольку в качестве элементов памяти используются триггера, то каждое состояние можно закодировать двоичным числом . Здесь a_i = {0, 1}, a Q – состояние автомата. Отсюда:

Общее число необходимых элементов памяти можно определить из следующего неравенства:, где (М + 1) – число состояний автомата.

В отличие от абстрактного автомата, имеющего один входной и один выходной каналы, на которые поступают сигналы во входном
X = {x₁, x₂,..., x_f,…, x_F} и выходном Y = {y₁, y₂,..., y_g,..., y_G} алфавитах, структурный автомат имеет L входных и N выходных каналов. Каждый входной x_j и выходной y_j сигналы абстрактного автомата могут быть закодированы двоичным набором состояний входных и выходных каналов структурного автомата: , .

Здесь и – значения двоичных входных и выходных сигналов соответственно. Число каналов L и N можно определить аналогичнo формуле для определения R:

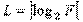
Изменение состояния элементов памяти происходит под действием сигналов U = (U₁, U₂,..., U_R), поступающих на их входы. Эти сигналы формируются комбинационной схемой КС1 и называются сигналами возбуждения элементарных автоматов. На вход КС1, кроме входных сигналов, по цепи обратной связи поступают сигналы Q = (Q₁, Q₂,..., Q_r,..., Q_R) с выходов элементов памяти автомата. Комбинационная схема КС2 служит для формирования выходных сигналов Y = {y₁, y₂,..., y_g,..., y_G}, причем в случае автомата Мили на вход этой схемы поступают входные сигналы, а в случае автомата Мура – входные сигналы не поступают.

Поиск по сайту: