АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Связь между дифференцируемостью и существованием частных производных

Читайте также:
  1. D) постоянных затрат к разнице между ценой реализации продукции и удельными переменными затратами.
  2. I Раздел 1. Международные яиившжоши. «пююеям как процесс...
  3. I. О различии между чистым и эмпирическим познанием
  4. II. Типы отношений между членами синтагмы
  5. III. Разрешение споров в международных организациях.
  6. IV. Двойная связь и конверсия
  7. IV. О различии между аналитическими и синтетическими суждениями
  8. Автогенератор с емкостной обратной связью
  9. Анализ взаимосвязей между показателями эффективности инвестиционно-инновационных проектов и показателями эффективности хозяйственной деятельности предприятия
  10. Анализ взаимосвязи между обобщающими, частными показателями экономической эффективности деятельности предприятия и эффективностью каждого научно-технического мероприятия
  11. Анализ затрат с учетом международных стандартов
  12. Анализ равновесия между активами предприятия и источниками их формирования. Оценка финансовой устойчивости предприятия

Напомним, что для функций одной переменной существование производной в точке 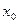является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функций многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами.

Теорема 1(необходимое условие дифференцируемости). Если функция дифференцируема в точке 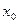, то у нее в точке 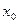существуют все частные производные. При этом 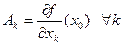, и тем самым

,

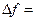
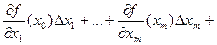
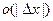где = .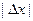

Обратная теорема неверна, т.е. существование частных производных не является достаточным условием дифференцируемости функции.

Пример 1. Рассмотрим функцию

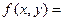
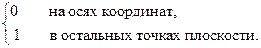
Функция в точке 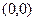разрывна, поэтому она в точке 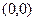не может быть дифференцируемой. Так как 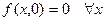, и , то существуют и равны нулю 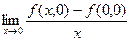и , а это и есть 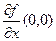и 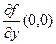соответственно.

Теорема 2 (достаточное условие дифференцируемости).

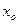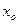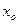Если функция в некоторой окрестности точки имеет все частные производные и эти производные в точке непрерывны, то функция в точке дифференцируема.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)